  |
| Politica de confidentialitate |
|
|
| • domnisoara hus • legume • istoria unui galban • metanol • recapitulare • profitul • caract • comentariu liric • radiolocatia • praslea cel voinic si merele da aur | |
ELECTROMAGNETI
Electromagnetii sunt ansambluri larg utilizate in electrotehnicǎ sau/si in automaticǎ, intervenind atat ca surse de energie, fiind bine adaptati pentru actionarea aparatelor electromagnetice de comutatie, cat si ca elemente de protectie relee) sau de automatizare (executie).
1. Generalitǎti. Clasificare. Variante constructive si pǎrti componente
Electromagnetii sunt definiti ca fiind dispozitive, care transformǎ energia electricǎ primitǎ de o bobinǎ de la o sursǎ de alimentare, in energie a campului magnetic, localizatǎ mai ales la nivelul intrefierului de lucru si concretizatǎ in actiuni mecanice (forte sau cupluri) care pot realiza deplasǎri utile, predeterminate si univoce, in sensul micsorǎrii intrefierului.
Sursa de alimentare poate fi de tensiune sau de curent, cu functionare in curent continuu sau in curent alternativ.
Principalele pǎrti componente ale electromagnetilor, ce pot fi identificate in Fig. II-1, sunt :
bobina (de tensiune sau de curent), 1, care este eventual amplasatǎ pe o carcasǎ ;
miezul feromagnetic, ce cuprinde elemente fixe, 2, dar si elemente mobile, cum este armǎtura mobilǎ, 3, (cu miscare de rotatie sau de translatie);
intrefierul de lucru, 4, (existǎ si intrefieruri parazite, mult mai mici), situat intre elementele fixe si cele mobile ale miezului.
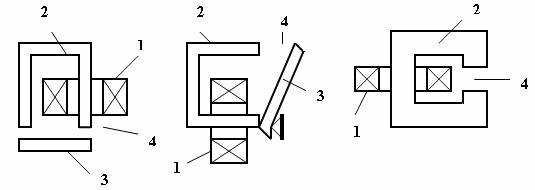
Fig. II-1 : Pǎrtile componente ale unui electromagnet
-bobina, 2-miezul feromagnetic, 3-armǎtura mobilǎ, 4-intrefier
Se remarcǎ faptul cǎ in cazul ultimului desen din Fig. II-1 lipseste armǎtura mobilǎ, electromagnetii fiind uneori folositi pentru a genera un camp magnetic in zona intrefierului. In plus semnalǎm faptul cǎ portiunile feromagnetice ale miezului, situate fatǎ in fatǎ in zona intrefierului se numesc piese polare.
Variantele de electromagneti prezentate in desenele anterioare corespund unor miezuri feromagnetice neramificate, dar in Fig. II-2 prezentǎm exemple de electromagneti cu circuit magnetic ramificat, de tip E-I cu armǎturǎ mobilǎ exterioarǎ bobinei si respectiv de tip plonjor, cu armǎturǎ mobilǎ interioarǎ bobinei. In cazul electromagnetului de tip plonjor, acesta poate functiona chiar cu circuit magnetic deschis, cand va avea doar bobina 1 si plonjorul 3.
Bobina electromagnetului poate fi unicǎ, sau divizatǎ in douǎ semibobine conectate de obicei in serie. Semnalǎm in plus faptul c. 2; asemenea circuite magnetice pot fi simetrice sau asimetrice.
Functionarea electromagnetilor este influentatǎ de geometria miezului feromagnetic. Astfel pentru electromagnetii cu armǎturǎ mobilǎ interioarǎ bobinei, fluxurile magnetice de dispersie contribuie la realizarea fortelor (cuplurilor) mecanice active, in timp ce pentru elecctromagnetii cu armǎturǎ mobilǎ exterioarǎ bobinei aceste fluxuri reprezintǎ doar pierderi magnetice. De asemenea pentru situatiile in care bobina este dispusǎ pe dimensiunea mai mare a miezului feromagnetic (adesea nu se poate evita acest lucru din considerente tehnologice), se impune calculul magnetic cu considerarea solenatiei aferente ca fiind uniform distribuitǎ, fǎrǎ a beneficia de avantajele ipotezei care o considerǎ concentratǎ, deoarece erorile de calcul devin prea mari.
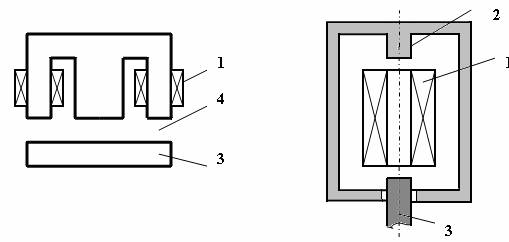
Fig. II-2 : Electromagneti cu circuit magnetic ramificat
-bobina, 2-opritorul, 3-armǎtura mobilǎ, 4-intrefierul de lucru
Din punctul de vedere al constructiei si functionǎrii miezului feromagnetic, electromagnetii pot fi realizati cu o singurǎ sursǎ de solenatie (bobinǎ) , asa cum s-a prezentat anterior, dar si cu mai multe surse de solenatie (bobine sau magneti permanenti), cand sunt numiti electromagneti polarizati, v. Fig. II-3.
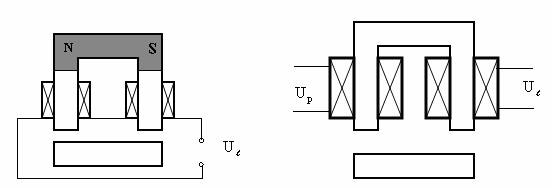
Fig. II-3 : Electromagneti polarizati
In primul desen sursa de solenatie de polarizare este un magnet permanent (N-S), iar in al doilea sursa de polarizare este o bobinǎ alimentatǎ de la o sursǎ de tensiune continuǎ, Up, la acestea adǎugandu-se solenatia generatǎ de infǎsurǎrile de lucru, alimentate de lasursa de tensiune Ul. Prezenta sursei de polarizare conferǎ particularitǎti functionale speciale pentru electromagnatii polarizati, care sunt sensibili la sensul mǎrimii de lucru si eventual pot "memora" ultima stare de functionare.
Clasificarea electromagnetilor d.p.d.v. al miezului feromagnetic mai evidentiazǎ posibilitatea realizǎrii acestuia din fier masiv (de obicei in c.c.) sau din tole (obisnuit in c.a.).
Clasificarea electromagnetilor poate considera de asemenea si circuitul bobinei, deosebind pe de o parte electromagneti cu bobinǎ de tensiune (cu spire numeroase si subtiri) si respectiv electromagneti cu bobinǎ de curent (cu spire putine, iar la limitǎ una singurǎ si cu rezistentǎ electricǎ mai micǎ desigur fatǎ de bobinele de tensiune), acestia putand functiona in c.c. sau in c.a., in primul caz bobina fiind "inaltǎ" sau "suplǎ" in timp ce in al doilea caz bobina este de obicei "joasǎ".
Dupǎ valorile timpului de actionare electromagnetii pot fi:
ultrarapizi, cu actionare in timp de ordinul milisecundelor (de obicei electromagnetii polarizati);
rapizi, cu timpi de actionare de ordinul 10-2 secunde, (de obicei electromagnetii de c.a.);
lenti, cu timpi de actionare de ordinul 0,1-0,2 secunde, (de obicei electromagnetii de c.c.).
Dupǎ ipotezele care pot fi acceptate in legǎturǎ cu studiul lor, electromagnetii pot functiona cu solenatie constantǎ (ipotezǎ valabilǎ pentru electromagnetii de c.c.) sau cu flux constant (ipotezǎ preferatǎ pentru electromagnetii de c.a.).
In virtutea celor prezentate mai sus, se remarcǎ impresionanta variatate de forme constructive de electromagneti, utilizati intr-o gamǎ incǎ mai largǎ de tipodimensiuni, adaptate pentru o mare diversitate de aplicatii, clasice sau ultramoderne.
Mǎrimi si relatii de bazǎ in studiul electromagnetilor
Elementele de bazǎ ale unui electromagnet sunt:
bobina, care reprezintǎ circuitul electric;
miezul, care reprezintǎ circuitul magnetic;
armǎtura mobilǎ si accesoriile aferente, care reprezintǎ ansamblul mecanic.
In cele ce urmeazǎ vom urmǎri succesiv mǎrimile si relatiile de bazǎ ce intervin in studiul acestor componente, ca si particularitǎtile specifice lor.
1. Mǎrimi si relatii de bazǎ cu privire la circuitul electric al electromagnetilor
Circuitul electric al electromagnetilor se referǎ desigur la circuitul bobinei acestora, care este o bobinǎ realǎ (cu rezistentǎ de "pierderi"), cǎreia i se poate atasa o schemǎ echivalentǎ serie sau derivatie, cum se aratǎ in Fig. II-4.
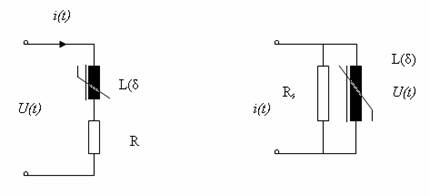
Fig. II-4 : Scheme echivalente pentru circuitul electric al electromagnetilor
In cele ce urmeazǎ ne vom referi doar la schema echivalentǎ derivatie, atasatǎ electromagnetilor cu bobinǎ de tensiune, dar concluziile si observatiile pot fi cu usurintǎ adaptate pentru schema echivalentǎ serie, proprie bobinelor de curent.
Deplasarea armǎturii mobile in timpul functionǎrii electromagnetilor, dupǎ o lege de miscare δ(t), face ca valorile inductantei bobinei, L[δ(t)], sǎ se modifice de asemenea in timp, conform unei relatii care, pentru un miez de tip U-I, v. Fig. II-1, este de forma:
![]() , (II-1)
, (II-1)
care devine succesiv:
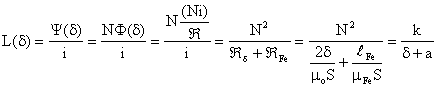 , (II-2)
, (II-2)
in care N este numǎrul de spire al
bobinei, ![]()
![]() -fluxul magnetic total,
-fluxul magnetic total, ![]() -fluxul magnetic ( cu relatia cunoscutǎ
-fluxul magnetic ( cu relatia cunoscutǎ ![]() ), i-curentul ce parcurge spirele bobinei, δ-valoarea
intrefierului,
), i-curentul ce parcurge spirele bobinei, δ-valoarea
intrefierului, ![]() -lungimea circuitului magnetic din fier a pentru miezul
considerat, µo si µFe-permeabilitatea magneticǎ a
aerului din intrefier si respectiv a fierului din miezul de sectiune
transversalǎ S, astfel incat constantele "k" si "a" au in acest caz expresiile:
-lungimea circuitului magnetic din fier a pentru miezul
considerat, µo si µFe-permeabilitatea magneticǎ a
aerului din intrefier si respectiv a fierului din miezul de sectiune
transversalǎ S, astfel incat constantele "k" si "a" au in acest caz expresiile:
![]() , respectiv
, respectiv ![]() . (II-3)
. (II-3)
Curba tipicǎ de variatie a inductantei L a bobinei unui electromagnet in raport cu intrefierul δ, este de forma prezentatǎ in Fig. II-5.
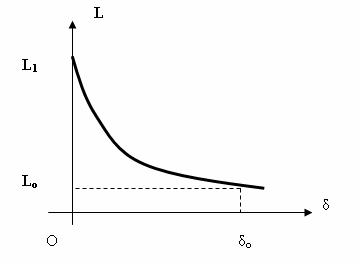
Fig. II-5 : Dependenta inductantei bobinei de intrefier la electromagneti
Ecuatia care descrie comportarea electricǎ a circuitului bobinei unui electromagnet atunci cand armatura sa mobilǎ nu se deplaseazǎ (deci pentru pozitia sa initialǎ la intrefier maxim, δo sau pentru pozitia sa finalǎ de "actionat", se poate scrie sub forma:
![]() sau
sau ![]() , (II-4)
, (II-4)
in timp ce pentru durata miscǎrii armǎturii mobile aceastǎ ecuatie se preferǎ a fi scrisǎ sub forma:
![]() sau
sau ![]() , (II-5)
, (II-5)
respectiv sub forma echivalentǎ:
![]() , cu
, cu ![]() , (II-6)
, (II-6)
care pune in evidenta viteza "v" de deplasare a armǎturii mobile, astfel incat cu cat aceastǎ vitezǎ este mai mare, perturbatiile de comportare electricǎ datorate miscǎrii, vor fi mai importante.
De
remarcat faptul cǎ valorile inductantei bobinei electromagnetilor, depind
si de valorile curentului ce parcurge spirele bobinei, deci de fapt de nivelul
de saturatie a miezului feromagnetic. Dacǎ se acceptǎ aproximarea
caracteristicii ![]() cu o parabolǎ
cubicǎ:
cu o parabolǎ
cubicǎ:
![]() , (II-7)
, (II-7)
rezultǎ :
![]() . (II-8)
. (II-8)
Dacǎ
se considerǎ curbele ![]() pentru valori diferite
ale intrefierului, δo>δ1>>δn
pentru valori diferite
ale intrefierului, δo>δ1>>δn![]() , date in Fig. II-6, actionarea corespunde trecerii de
la curba corespunzǎtoare intrefierului initial, δo, la
intrefierul final δn, care se realizeazǎ dupǎ curba
3.
, date in Fig. II-6, actionarea corespunde trecerii de
la curba corespunzǎtoare intrefierului initial, δo, la
intrefierul final δn, care se realizeazǎ dupǎ curba
3.
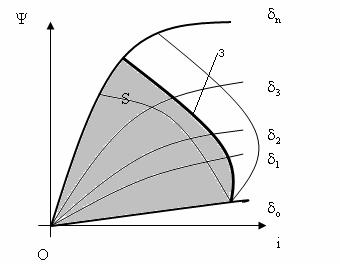
Fig. II-6 : Cu privire la actionarea electromagnetilor
Lucrul mecanic ce poate fi efectuat de armǎtura mobilǎ a electromagnetului la "actionare" este proportional cu suprafata "S", (hasuratǎ) din desenul alǎturat, iar modul de trecere de la intrefierul iniintrefierul intial la cel final poate urmǎri oricare dintre curbele sugerate, cu respectarea eventualǎ a ipotezelor de functionare anuntate anterior, la flux constant sau la solenatie constantǎ (curent constant).
Mǎrimi si relatii de bazǎ pentru circuitul magnetic al electromagnetilor
Circuitul magnetic al electromagnetilor, reprezintǎ un ansamblu de materiale feromagnetice, care asigurǎ suportul fizic pentru trecerea fluxului magnetic cǎtre zona activǎ a intrefierului de lucru, pe seama solenatiei proprii bobinei ale cǎrei spire sunt parcurse de curentul "i". Practic bobina electromagnetilor este deci un element dual, care intervine prin parametrii R si L(δ) in circuitul electric de alimentare, respectiv prin solenatia produsǎ in circuitul magnetic de cele "N" spire, F = Ni.
Calculul circuitelor
magnetice are la bazǎ analogia electric-magnetic, care face sǎ
corespundǎ fluxul magnetic ![]() - curentului I, reluctanta magneticǎ
- curentului I, reluctanta magneticǎ ![]() - rezistentei R si
respectiv solenatia F - tensiunii electromotoare E.
- rezistentei R si
respectiv solenatia F - tensiunii electromotoare E.
Fluxul magnetic ![]() [Wb], se poate calcula
cu relatia:
[Wb], se poate calcula
cu relatia:
![]() [Wb] , (II-9)
[Wb] , (II-9)
unde B [T] reprezintǎ inductia magneticǎ, iar S [m2]-sectiunea transversalǎ a miezului feromagnetic.
Legea lui Ohm pentru circuite magnetice, care permite definirea cǎderii de tensiune magneticǎ, Um, se scrie:
Um
= ![]() [A] , (II-10)
[A] , (II-10)
in care reluctanta magneticǎ, pentru o
portiune omogenǎ si izotropǎ de material feromagnetic avand lungimea ![]() , sectiunea transversalǎ S si permeabilitatea
magneticǎ µ, este:
, sectiunea transversalǎ S si permeabilitatea
magneticǎ µ, este:
![]() . (II-11)
. (II-11)
Pentru
o portiune de circuit magnetic de lungime ![]() si de sectiune
variabilǎ, cum se prezintǎ in Fig. II-7, reluctanta magneticǎ
si de sectiune
variabilǎ, cum se prezintǎ in Fig. II-7, reluctanta magneticǎ ![]() se evalueazǎ cu
ajutorul relatiei:
se evalueazǎ cu
ajutorul relatiei:
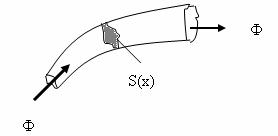
Fig. II-7 : Cu privire la reluctanta magneticǎ
![]() , (II-12)
, (II-12)
unde µ(x) se defineste considerand succesiv, pentru fiecare valoare a sectiunii transversale S(x), inductia magneticǎ B(x), intensitatea campului magnetic, H(x), corespunzǎtoare caracteristicii de magnetizare B(H) a materialului miezului si raportul lor, folosind relatiile:
![]() , H(x) folosind curba B(H) ,
, H(x) folosind curba B(H) , ![]() . (II-13)
. (II-13)
Inversul
reluctantei magnetice ![]() , reprezintǎ permeanta magneticǎ, Λ:
, reprezintǎ permeanta magneticǎ, Λ:
![]() . (II-14)
. (II-14)
Semnalǎm faptul cǎ in zona de trecere a fluxului magnetic de la piesele feromagnetice la intrefieruri (aer), intervine "umflarea" liniilor de camp magnetic, ceea ce face mai dificilǎ evaluarea premeantelor (a reluctantelor) aferente.
In cazul circuitelor magnetice ramificate se folosesc teoremele lui Kirchhoff pentru circuite magnetice, care se enuntǎ astfel:
suma algebricǎ a fluxurilor
magnetice ![]() , incidente unui nod de circuit magnetic, este nulǎ, ce
reprezintǎ prima teoremǎ a lui Kirchhoff pentru circuite magnetice:
, incidente unui nod de circuit magnetic, este nulǎ, ce
reprezintǎ prima teoremǎ a lui Kirchhoff pentru circuite magnetice:
![]() ; (II-15)
; (II-15)
suma algebricǎ a
cǎderilor de tensiune magneticǎ, ![]() , ce intervin pe ramurile unui ochi al unui circuit magnetic
ramificat, este egalǎ cu suma algebricǎ a solenatiilor
, ce intervin pe ramurile unui ochi al unui circuit magnetic
ramificat, este egalǎ cu suma algebricǎ a solenatiilor ![]() , surselor care intervin pe acele ramuri:
, surselor care intervin pe acele ramuri:
![]() . (II-16)
. (II-16)
Calculul unui circuit magnetic neramificat de tip U-I, de tipul celui prezentat in Fig. II-1, apeleazǎ la o schemǎ magneticǎ echivalentǎ de forma celei din Fig. II-8.
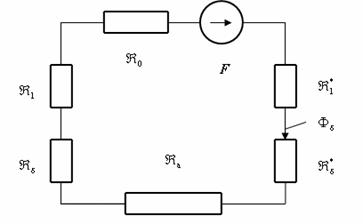
Fig. II-8 : Schema magneticǎ echivalentǎ pentru un electromagnet
Schema
magneticǎ echivalentǎ a circuitului magnetic pentru un electromagnet
de tip U-I, datǎ mai sus, implicǎ acceptarea ipotezelor cu privire la
considerarea parametrilor circuitului magnetic ca fiind concentrati (desi
acestia sunt de fapt uniform distribuiti), ca si neglijarea fluxurilor
magnetice de dispersie (desi dispersia magneticǎ este de fapt
importantǎ, in conditiile in care gradul de comutatie magneticǎ este
de doar 103-105, fatǎ de gradul de comutatie
electricǎ cu contacte, care este de 1010-1014).
Parametrii concentrati ai miezului magnetic intervin in schema magneticǎ echivalentǎ
prin reluctante magnetice (![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() sau
sau![]() ), dar si prin solenatia concentratǎ, F (care fizic
este uniform distribuitǎ, pe coloana pe care este amplasatǎ bobina). De
subliniat faptul cǎ evaluarea reluctantelor magnetice ale intrefierurilor
trebuie sǎ considere "umflarea" liniilor de camp magnetic in zona de
trecere de la miezul feromagnetic la zona de aer, ceea ce implicǎ
considerarea unor suprafete de calcul pentru piesele polare, conform
metodei Roters.
), dar si prin solenatia concentratǎ, F (care fizic
este uniform distribuitǎ, pe coloana pe care este amplasatǎ bobina). De
subliniat faptul cǎ evaluarea reluctantelor magnetice ale intrefierurilor
trebuie sǎ considere "umflarea" liniilor de camp magnetic in zona de
trecere de la miezul feromagnetic la zona de aer, ceea ce implicǎ
considerarea unor suprafete de calcul pentru piesele polare, conform
metodei Roters.
Semnalǎm
si forma discretǎ a legii circuitului magnetic, aplicabilǎ
pentru calcululmai precis al miezului electromagnetilor, care substituie
integrala cunoscutǎ cu sume, ce se referǎ la "n" portiuni ale
circuitului magnetic, de lungime ![]() si parcurse de campul
magnetic Hi, scrisǎ sub forma:
si parcurse de campul
magnetic Hi, scrisǎ sub forma:
![]() , (II-17)
, (II-17)
unde C este conturul pe care se inchid liniile
de camp magnetic, cu observatia cǎ de fapt produsul (Hi![]() ) reprezintǎ cǎderea de tensiune
magneticǎ pe portiunea "i" a circuitului magnetic. De remarcat si cǎ
aceastǎ formǎ a legii circuitului magnetic substituie parametrii
concentrati cu parametri distribuiti, ce corespund practic unei partitii de
calcul asociate circuitului magnetic real.
) reprezintǎ cǎderea de tensiune
magneticǎ pe portiunea "i" a circuitului magnetic. De remarcat si cǎ
aceastǎ formǎ a legii circuitului magnetic substituie parametrii
concentrati cu parametri distribuiti, ce corespund practic unei partitii de
calcul asociate circuitului magnetic real.
Calculul circuitelor magnetice aferente electromagnetilor decurge cu o precizie acceptabilǎ dacǎ se considerǎ neliniaritatea caracteristicii de magnetizare a materialului miezului feromagnetic B(H) si dispersia magneticǎ.
Acest calcul este mai rapid pentru circuite magnetice neramificate, dar laborios pentru circuite magnetice ramificate si eventual asimetrice.
Progresele tehnicii de calcul au permis dezvoltarea unor metode numerice pentru abordarea problemelor specifice campurilor (electrice, magnetice sau termice), cum sunt metoda elementelor finite sau, mai nou, metoda volumelor finite de exemplu.
Semnalǎm de asemenea faptul cǎ la functionarea in cure nt alternativ a circuitelor magnetice si mai ales in cazul utilizǎrii spirelor in scurtcircuit, intervine obisnuit un defazaj intre mǎrimile magnetice aferente miezului feromagnetic (solenatie si flux magnetic), care de obicei este ignorat in calculul acestora, cu exceptia situatiilor in care ne referim la aplicatii speciale.
1. Punct optim de functionare pentru un circuit magnetic neramificat
Se considerǎ un electromagnet cu miez de tip U-I, prevǎzut cu o bobinǎ de tensiune care produce o solenatie F, alimentat de la o sursǎ de tensiune continuǎ, asa cum este cel prezentat in Fig. II-9.
Fig. II-9 : Cu privire la punctul optim de functionare pentru un miez magnetic
In cazul electromagnetilor, energia campului magnetic, Wmagnδ, este localizatǎ in principal la nivelul intrefierului de lucru, δ, avand o valoare care anuntǎ potentialul lucru mecanic ce se poate efectua prin deplasarea armǎturii lor mobile, energie care este deci de dorit a fi cat mai mare, pentru o configuratie datǎ a miezului magnetic, putandu-se evalua cu ajutorul relatiei:
![]() , (II-18)
, (II-18)
putandu-se afirma cǎ aceasta este
proportionalǎ cu produsul (![]() ). Dacǎ se impune conditia ca derivata sǎ fie
nulǎ, ceea ce implicǎ valori de extrem pentru Wmagnδ:
). Dacǎ se impune conditia ca derivata sǎ fie
nulǎ, ceea ce implicǎ valori de extrem pentru Wmagnδ:
![]() , (II-19)
, (II-19)
se obtine:
![]() si deci
si deci ![]() , (II-20)
, (II-20)
cu semnificatia cǎ existǎ o
interdependentǎ intre pozitia armaturii mibile, δ si valoarea
fluxului magnetic din miez, ![]() .
.
Dacǎ se considerǎ acum solenatia dezvoltatǎ de bobina electromagnetului, F, ca avand o componentǎ corespunzǎtoare circuitului magnetic din fier, FFe si o componentǎ corespunzǎtoare intrefierului de lucru, Umδ, se poate scrie relatia:
F = FFe + Umδ , (II-21)
care, dupǎ impǎrtirea la lungimea
circuitului magnetic din fier, ![]() , defineste solenatia raportatǎ, f, rezultand:
, defineste solenatia raportatǎ, f, rezultand:
f
= HFe + fδ , cu f = F/![]() , HFe = FFe/
, HFe = FFe/![]() , fδ
=Umδ/
, fδ
=Umδ/![]() . (II-22)
. (II-22)
Deoarece
se acceptǎ obisnuit cǎ functionarea electromagnetilor de curent
continuu decurge la solenatie constantǎ, prin derivarea relatiei (II-21)
in raport cu variabila ![]() se obtine:
se obtine:
![]() , (II-23)
, (II-23)
ce se poate scrie sub forma echivalentǎ:
![]() . (II-24)
. (II-24)
Considerand acum relatiile:
dFFe
=d(![]() )=
)= ![]() dHFe si d
dHFe si d![]() = S dBFe , (II-25)
= S dBFe , (II-25)
conditia (II-24) devine:
![]() (II-26)
(II-26)
Valorile tgβ sunt evident constante, pentru o configuratie datǎ a miezului feromagnetic, iar punctul optim de functionare pentru acest miez feromagnetic, este acela pentru care tangenta la caracteristica de magnetizare a materialului magnetic, B(H), are panta tgβ, unghi care este respectat si de dreapta care uneste punctul de abscisǎ f, cu punctul de functionare, M, vezi Fig. II-10.
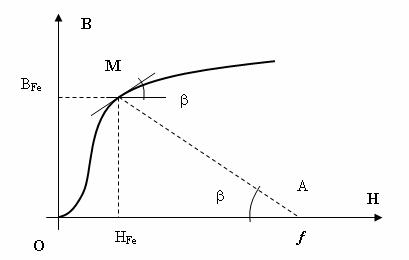
Fig. II-10 : Cu privire la punctul optim de functionare pentru
un miez feromagnetic neramificat
Semnalǎm faptul cǎ, pe seama considerentelor prezentate mai sus, stau la baza realizǎrii unui calcul expeditiv al circuitelor magnetice neramificate, cu o precizie acceptabilǎ, folosind metoda raportǎrii.
Principalele probleme care se pun cu privire la calculul unor asemenea circuite magnetice (cu armǎturǎ mobilǎ exterioarǎ bobinei), sunt legate de considerarea neliniaritǎtii caracteristicii de magnetizare a materialului miezului, respectiv de considerarea dispersiei magnetice, cu dificultǎti deosebite pentru cazul circuitelor magnetice ramificate nesimetrice.
Pentru miezurile feromagnetice ale electromagnetilor de c.a. calculul decurge similar in primǎ aproximatie, dar uneori trebuie sǎ se tinǎ seama de reactanta magneticǎ, ce completeazǎ reluctanta magneticǎ consideratǎ obisnuit, care intervine pe seama infǎsurǎrilor (eventual in scurtcircuit) si care conduce la obtinerea unui anumit defazaj intre solenatia magneticǎ si fluxul magnetic din miez.
Calculul circuitelor magnetice cu armǎturǎ mobilǎ interioarǎ bobinei
Calculul unor asemenea circuite magnetice, specifice electromagnetilor de tip plonjor, v. Fig. II-11, trebuie sǎ considere interventia dispersiei magnetice, deoarece fluxurile de dispersie contribuie la realizarea fortei de atractie a acestora. In plus se impune si considerarea solenatiei infǎsurǎrii ca fiind uniform distribuitǎ, in concordantǎ cu sonstructia "suplǎ" sau "inaltǎ" a bobinei acestor electromagneti, ce sunt utilizati de obicei in c.c.
Miscarea plonjorului cilindric 4, de diametru "d", ce se poate deplasa in interiorul bobinei 6 (ce este plasatǎ pe carcasa 5), este ghidatǎ cu ajutorul unei tije metalice, 1, de diametru "do".
Dispersia
magneticǎ se realizeazǎ intre cilindrul plonjorului de diametru "d",
acelasi cu diametrul opritorului 3, de lungime "m", si cilindrul
interior de diametru "D" al miezului 2, pe toatǎ inǎltimea "hb"
a bobinei. Dacǎ se considerǎ permeanta de dispersie, ![]() , definitǎ de relatia:
, definitǎ de relatia:
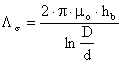 , (II-27)
, (II-27)
astfel incat permeanta raportatǎ de
dispersie, ![]() , rezultǎ:
, rezultǎ:
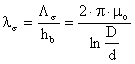 , (II-28)
, (II-28)
unde µo=4π 10-7 [H/m] reprezintǎ permeabilitatea magneticǎ a aerului.
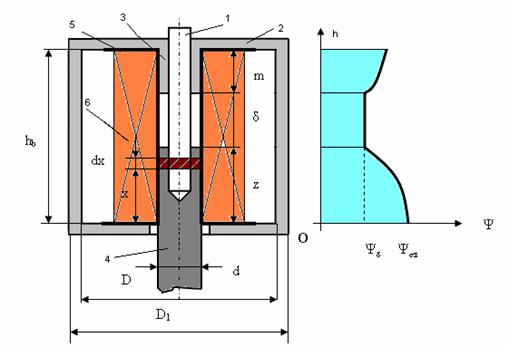
Fig. II-11 : Electromagnet plonjor cu armǎtura mobilǎ interioarǎ bobinei
Solenatia distribuitǎ a infǎsurǎrii, f, se poate calcula cu ajutorul relatiei:
![]() , (II-29)
, (II-29)
astfel incat fluxul de dispersie elementar d![]() , corespunzǎtor elementului infinitesimal dx, situat la
distanta x de la baza miezului, v. Fig. II-11, se scrie:
, corespunzǎtor elementului infinitesimal dx, situat la
distanta x de la baza miezului, v. Fig. II-11, se scrie:
![]() , (II-30)
, (II-30)
obtinandu-se, pentru lungimea z a plonjorului:
![]() . (II-31)
. (II-31)
Corespunzǎtor
fluxului magnetic total, considerand spirele bobinei uniform distribuite pe
inǎltimea hb ca fiind (![]() ), deci la nivelul lui
dx sunt
), deci la nivelul lui
dx sunt ![]() spire, rezultǎ succesiv:
spire, rezultǎ succesiv:
![]() , (II-32)
, (II-32)
care pentru intreg plonjorul de lungime z,
deci pentru x=0, devine, vezi si curba ![]() datǎ in Fig. II-12:
datǎ in Fig. II-12:
![]() . (II-33)
. (II-33)
Un
rationament similar la nivelul opritorului de lungime m, care defineste fluxul ![]() , permite sǎ scriem expresia fluxului magnetic total,
, permite sǎ scriem expresia fluxului magnetic total, ![]() , sub forma:
, sub forma:
![]() , (II-34)
, (II-34)
astfel incat este posibil sǎ apreciem
energia campului magnetic, ![]() :
:
![]() , (II-35)
, (II-35)
care evidentiazǎ atat contributia intrefierului de lucru cat si aportul opritorului si al plonjorului.
Mentionǎm cǎ expresia energiei campului magnetic, datǎ mai sus, poate fi utilizatǎ pentru a defini forta de atractie care actioneazǎ asupra plonjorului, asa cum se va vedea in Capitolul 3. 3.
3. Mǎrimi si relatii de bazǎ referitoare la ansamblul mecanic al electromagnetilor
Ansamblul mecanic al electromagnetilor cuprinde armǎtura mobilǎ a acestora, ca si toate elementele atasate acesteia, considerandu-le si pe cele cu rol de sustinere sau de ghidare a miscǎrii sale univoce.
Pentru evaluarea stǎrii de miscare la nivelul armǎturii mobile a unui electromagnet, se impune definirea actiunilor mecanice utile (forte sau cupluri de atractie), ca si a actiunilor mecanice rezistente, care se opun miscǎrii, (frecǎri, mase in miscare, resorturi antagoniste etc.). Astfel, pentru un aparat electromagnetic de comutatie, de tip contactor de c.a., cu miscare de translatie a ansamblului mobil (realizatǎ cu ajutorul unui electromagnet), asa cum sugereazǎ desenul din Fig. II-12a, diagramele fortelor active, F(δ) si rezistente, FR(δ) sunt date in Fig. II-12b.
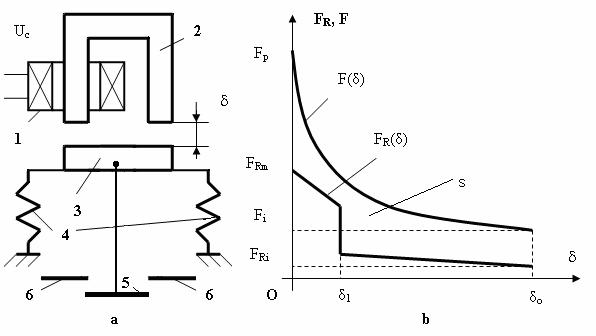
Fig. II-12 : Cu privire la ansamblul mecanic al unui electromagnet
Fortele active sunt reprezentate chiar de forta de atractie care intervine asupra armǎturii mobile 3 la alimentarea bobinei 1, datoritǎ magnetizǎrii miezului feromagnetic 2, tinzand sǎ micsoreze intrefierul δ, curba F(δ) fiind numitǎ si caracteristicǎ electromecanicǎ a electromagnetului. Fortele rezistente sunt cele de greutate, de frecare, sau datorate resorturilor elastice, cum sunt cele "antagoniste" 4 (care contribuie la cursa de revenire a armǎturii mobile in pozitia initialǎ dupǎ o actionare). La atragerea armǎturii mobile a electromagnetului, se deplaseazǎ si traversa contactelor mobile, 5, care realizeazǎ atingerea pieselor fixe de contact, 6, la o valoare δ1 a intrefierului, apelandu-se in acest caz la ruperea dublǎ a arcului electric de comutatie.
Miscarea ansamblului mobil (a armǎturii mobile a electromagnetului), este definitǎ practic de suprafata S dintre curbele F(δ) si FR(δ), fiind conditionatǎ de valori ale fortelor active superioare fortelor rezistente (forta portantǎ a electromagnetului, Fp, mai mare decat forta rezistentǎ maximǎ, FRm, dar si forta activǎ initialǎ, Fi, mai mare decat forta rezistentǎ initialǎ, FRi).
Considerandu-se o masǎ de miscare echivalentǎ, m*, eventual masa redusǎ conform analizei cinematice a ansamblului, ecuatia de miscare la actionare, care decurge dupǎ directia x, in sensul micsorǎrii intrefierului, se poate scrie sub forma:
![]() , (II-36)
, (II-36)
unde componenta ![]() se referǎ fortele
rezistente de naturǎ vascoasǎ ce depind de viteza de deplasare la un
exponent supraunitar, kx - forta elasticǎ a resortului antagonist, F(x) -
caracteristica electromecanicǎ a electromagnetului, iar FR(x) -
totalitatea celorlalte forte rezistente ce se opun miscǎrii. Aceasta este
evident o ecuatie diferentialǎ neliniarǎ (eventual cu coeficienti
variabili, cum este m* in anumite situatii), care sugereazǎ totusi faptul
cǎ aceastǎ comportare mecanicǎ, concretizatǎ in solutia
x(t), depinde esential de comportarea electricǎ, prin valorile curentului
din circuitul bobinei, ale inductantei bobinei, L(δ), respectiv ale
fluxului magnetic din miez, acestea fiind la randul lor influentate de
comportarea ansamblului mecanic, asa cum indicǎ relatia (II-6).
se referǎ fortele
rezistente de naturǎ vascoasǎ ce depind de viteza de deplasare la un
exponent supraunitar, kx - forta elasticǎ a resortului antagonist, F(x) -
caracteristica electromecanicǎ a electromagnetului, iar FR(x) -
totalitatea celorlalte forte rezistente ce se opun miscǎrii. Aceasta este
evident o ecuatie diferentialǎ neliniarǎ (eventual cu coeficienti
variabili, cum este m* in anumite situatii), care sugereazǎ totusi faptul
cǎ aceastǎ comportare mecanicǎ, concretizatǎ in solutia
x(t), depinde esential de comportarea electricǎ, prin valorile curentului
din circuitul bobinei, ale inductantei bobinei, L(δ), respectiv ale
fluxului magnetic din miez, acestea fiind la randul lor influentate de
comportarea ansamblului mecanic, asa cum indicǎ relatia (II-6).
Rezultǎ deci cǎ utilizarea ecuatiei care descrie comportarea electricǎ a circuitului bobinei electromagnetilor este oportunǎ dacǎ se cunoaste legea de miscare a armǎturii lor mobile, in timp ce utilizarea ecuatiei de miscare a ansamblului mobil se poate folosi dacǎ se cunoaste comportarea electricǎ a circuitului bobinei (functionand in curent sinusoidal de exemplu).
3. 1. Electromagnetii ca sisteme electromecanice de conversie a energiei
Interdependentele intre miscarea armǎturii lor mobile si comportarea electricǎ a circuitului bobinei care se manifestǎ in functionarea electromagnetilor, sugereazǎ faptul cǎ este mai riguros ca aceste dispozitive sǎ fie privite ca un tot unitar.
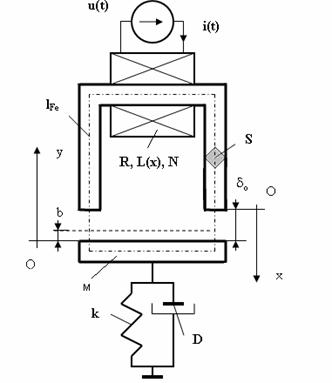
Fig. II-13 : Electromagnetul U-I ca sistem electromecanic de conversie a energiei
In acest scop se propune considerarea electromagnetilor ca fiind sisteme electromecanice de conversie a energiei, cu douǎ grade de libertate, unul electric /sarcina electricǎ q(t), curentul electric i(t) sau fluxul magnetic total ψ(t)/ si unul mecanic /deplasarea x(t) a armǎturii mobile/, pentru care sunt valabile ecuatii de tip Lagrange din mecanica analiticǎ:
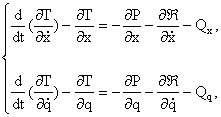 (II-37)
(II-37)
unde T(![]() reprezintǎ energia cineticǎ a sistemului:
reprezintǎ energia cineticǎ a sistemului:
![]() , (II-38)
, (II-38)
P(x,q) reprezintǎ energia potentialǎ a sistemului electromecanic:
![]() , (II-39)
, (II-39)
![]() reprezintǎ
functia de disipatie Rayleigh:
reprezintǎ
functia de disipatie Rayleigh:
![]() , (II-40)
, (II-40)
iar Qx si Qq sunt fortele generalizate corespunzǎtoare coordonatelor generalizate, x(t) respectiv q(t):
![]() ,
, ![]() . (II-41)
. (II-41)
In relatiile anterioare mai intervin notatii uzuale, care se recunosc cu usurintǎ dacǎ examinǎm electromagnetul din Fig. II-13 si anume: M care este masa armǎturii mobile a electromagnetului, L(x) - inductanta bobinei electromagnetului, ale cǎrei valori depind de valorile intrefierului dupǎ cum indicǎ curba din Fig. II-5, k - constanta elasticǎ a resortului antagonist prins pe armǎtura mobilǎ, b - pozitia armǎturii mobile pentru care resortul acesta nu este tensionat, R - rezistenta electricǎ a bobinei electromagnetului, D - constanta de amortizare mecanicǎ vascoasǎ a armǎturii mobile, g - acceleratia grevitationalǎ, u(t) - tensiunea de alimentare a bobinei electromagnetului.
Tinand seama de relatiile de mai sus, sistemul de ecuatii (II-37) se scrie sub forma:
![]()
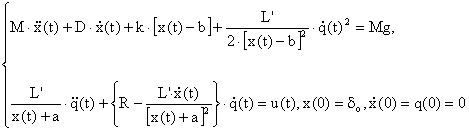 (II-42)
(II-42)
unde s-a aproximat dependenta L(x) cu o relatie de forma:
![]() , (II-43)
, (II-43)
cu constantele L' si a ce se pot defini folosind curba L(δ) corespunzǎtoare electromagnetului considerat, de forma indicatǎ in Fig. II-5, obtinandu-se final:
![]() si
si ![]() . (II-44)
. (II-44)
Dacǎ se foloseste drept coordonatǎ generalizatǎ electricǎ fluxul magnetic total, ψ(t):
![]() , (II-45)
, (II-45)
sistemul de ecuatii (II-42) se scrie :
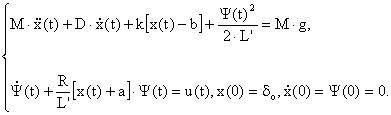 (II-46)
(II-46)
Sermnalǎm faptul cǎ functionarea electromagnetilor poate decurge la actionare fie pornind de la armǎtura mobilǎ in echilibru mecanic in pozitia initialǎ, de intrefier maxim δo, cand avem o functionare cu flux de pornire nul, (FPN), cand:
![]() , (II-47)
, (II-47)
fie cu armǎtura mobilǎ ce nu este in echilibru mecanic la intrefierul initial, cand avem o functionare cu flux de pornire nenul , (FPNN), cazul cel mai frecvent intalnit in practicǎ:
![]() , (II-48)
, (II-48)
valoarea fluxului magnetic "de pornire", ψp, calculandu-se cu ajutorul relatiei:
![]() cu
cu ![]() . (II-49)
. (II-49)
In cazul electromagnetilor ce functioneazǎ cu FPNN, acceptand schimbarea de variabilǎ, sustinutǎ si de notatiile din Fig. II-13:
![]()
![]()
![]() , (II-50)
, (II-50)
cu conditiile initiale care se scriu acum sub forma:
![]()
![]()
![]()
![]() , (II-51)
, (II-51)
si utilizand notatiile:
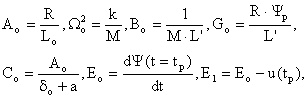 (II-52)
(II-52)
sistemul de ecuatii diferentiale neliniare (II-46), ce descrie comportarea electromagnetului considerat cu FPNN, la deplasarea armǎturii sale mobile, devine de forma:
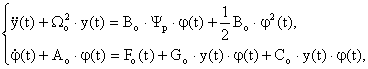 (II-53)
(II-53)
unde:
![]() dacǎ
u(t)=U=const. si respectiv (II-54)
dacǎ
u(t)=U=const. si respectiv (II-54)
![]() dacǎ
u(t)=Usin(ωt+
dacǎ
u(t)=Usin(ωt+![]() ) ,
) ,
sau de forma:
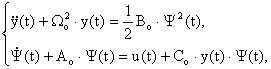 (II-55)
(II-55)
pentru electromagnetii care functioneazǎ cu FPN.
Mentionǎm cǎ pentru electromagnetii care functioneazǎ cu FPNN actionarea se produce cu intarziere la pornire, dupǎ care incepe practic miscarea armǎturii lor mobile, in timp ce pentru electromagnetii care functioneazǎ cu FPN, miscarea armǎturii lor mobile incepe imediat ce este alimentat circuitul bobinei.
Procedand similar, se poate defini sistemul de ecuatii diferentiale neliniare ce descrie comportarea electromagnetilor la revenire pe durata miscǎrii armǎturii lor mobile, cu observatia cǎ la revenire electromagnetii functioneazǎ cu FPNN.
3. Caracteristica de tip releu pentru electromagneti
Sistemele de ecuatii diferentiale neliniare care descriu comportarea electromagnetilor, considerati ca sisteme electromecanice de conversie a energiei cu douǎ grade de libertate, pe durata deplasǎrii armǎturii lor mobile, pot fi folosite cu succes pentru analiza comportǎrii lor in regim tranzitoriu (la "actionare" sau la "revenire"), permitand chiar optimizarea constructiei acestor dispozitive, dar pun in evidentǎ si functionarea electromagnetilor in regim de "releu", care stǎ la baza realizǎrii unei game largi de relee electromagnetice.
Dacǎ se considerǎ un electromagnet de tip U-I de curent continuu, v. Fig. II-13, care functioneazǎ cu FPN, pentru care miscarea armǎturii sale mobile incepe imediat ce bobina acestuia este alimentatǎ si se acceptǎ modificarea crescǎtoare foarte lentǎ a tensiunii de alimentare, U, pentru fiecare valoare a acesteia vor corespunde perechi de valori (Yo, ψo) de regim stationar, ca solutii ale sistemului de ecuatii (II-55), care se scrie sub forma echivalentǎ:
![]() ,
, ![]() , (II-56)
, (II-56)
astfel incat rezultǎ succesiv:
![]() si respectiv
si respectiv ![]() , (II-57)
, (II-57)
ecuatia (II-57) definind practic una sau trei valori posibile pentru pozitia Yo a armǎturii mobile a electromagnetului, pentru o valoare datǎ a tensiunii de alimentare U.
Considerand acum functiile:
![]() cu
cu ![]() si
si ![]() , (II-58)
, (II-58)
cu reprezentarea graficǎ din Fig. II-14, pozitia armǎturii mobile va fi definitǎ prin punctele de intersectie dintre curbele f(yo) si paralelele la axa absciselor g(yo,U), rezultate practic pentru o succesiune de valori ale tensiunii de alimentare (U1, U2, , Un).
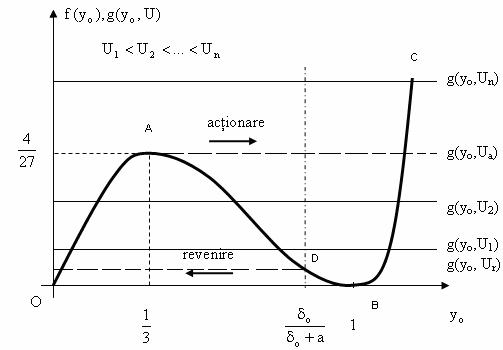
Fig. II-14 : Cu privire la caracteristica de tip releu pentru un electromagnet de c.c. cu FPN
Pentru
valorile lent crescǎtoare ale tensiunii de alimentare a circuitului
bobinei U1<U2<Ua, pozitia armǎturii
mobile va fi definitǎ prin valori yo<![]() , situate pe portiunea O-A. Punctul de extrem "A", de
ordonatǎ (
, situate pe portiunea O-A. Punctul de extrem "A", de
ordonatǎ (![]() ), premite chiar definirea tensiunii de actionare
sigurǎ, Ua, pentru electromagnetii de c.c. cu FPN, deoarece
pentru valoarea Ua a tensiunii de alimentare pozitia armǎturii
mobile evolueazǎ prin salt, teoretic panǎ la valori supraunitare, pe
portiunea B-C, practic panǎ la valoarea maximǎ posibilǎ fizic, (
), premite chiar definirea tensiunii de actionare
sigurǎ, Ua, pentru electromagnetii de c.c. cu FPN, deoarece
pentru valoarea Ua a tensiunii de alimentare pozitia armǎturii
mobile evolueazǎ prin salt, teoretic panǎ la valori supraunitare, pe
portiunea B-C, practic panǎ la valoarea maximǎ posibilǎ fizic, (![]() ), pe care o mentine pentru valori mai mari ale tensiunii de
alimentare, Ua<U<Un, ca stare "actionat".
Mentionǎm faptul cǎ portiunea A-B a curbei f(yo), cu
"pantǎ negativǎ", se referǎ la o comportare instabilǎ a
electromagnetului considerat.
), pe care o mentine pentru valori mai mari ale tensiunii de
alimentare, Ua<U<Un, ca stare "actionat".
Mentionǎm faptul cǎ portiunea A-B a curbei f(yo), cu
"pantǎ negativǎ", se referǎ la o comportare instabilǎ a
electromagnetului considerat.
Valoarea tensiunii de actionare sigurǎ a electromagnetului de curent continuu la functionarea cu FPN se poate evalua folosind conditia:
![]() sau
sau ![]() , (II-59)
, (II-59)
rezultand final:
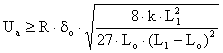 , (II-60)
, (II-60)
unde s-au considerat notatiile (II-58), astfel incat in formula datǎ intervin mǎrimi ce caracterizeazǎ electromagnetul, atat din punct de vedere mecanic, prin (k, δo), cat si din punct de vedere electric, (R, Lo, L1).
Pentru valori scǎzǎtoare ale tensiunii de alimentare a bobinei,Ur<U<Un, valorile teoretice ale deplasǎrii raportate a armǎturii mobile, yo, corespund portiunii C-D a curbei f(yo), dar practic se referǎ la paralela la axa ordonatelor ce trece prin punctul D, electromagnetul rǎmanand in starea "actionat".
Pentru valoarea Ur a tensiunii de alimentare a bobinei, se obtine practic revenirea, prin salt, a armǎturii mobile a electromagnetului considerat, in pozitia initialǎ, "neactionat", practic la un intrefier ce corespunde portiunii initiale a curbei, O-A.
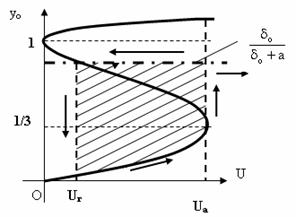
Fig. II-15 : Caracteristica de tip releu pentru electromagneti de c.c. cu FPN
Dacǎ
se traseazǎ curba corespunzǎtoare dependentei yo(U),
folosind desigur rezultatele obtinute cu ajutorul graficelor din Fig. II-14, se
obtine practic caracteristica de tip "releu" pentru un
electromagnet de curent continuu functionand cu FPN, care evidentiazǎ la
actionare o evolutie continuǎ a pozitiei yo in functie de
valorile U, panǎ la yo=1/3 si respectiv U=Ua,
dupǎ care, la atingerea valorii de actionare, Ua, sau la
scǎderea tensiunii sub valoarea de revenire, Ur, evolutia
pozitiei armǎturii mobile decurge prin salt (crescǎtor respectiv
scǎzǎtor), sugerat prin sǎgetile din Fig. II-15. Pentru valori Ur<U<Ua
electromagnetul poate fi practic neactionat, cu valori yo
cuprinse in domeniul (0, ![]() ), sau actionat, cu yo=δo/(δo+a)<1,
dupǎ cum se poate urmǎri in Fig. II-15.
), sau actionat, cu yo=δo/(δo+a)<1,
dupǎ cum se poate urmǎri in Fig. II-15.
Considerand acum un electromagnet de curent alternativ de tip U-I, v. Fig. II-13, care functioneazǎ cu FPN, la modificǎri foarte lente ale amplitudinii U a tensiunii alternative de alimentare a circuitului bobinei, u(t):
![]()
![]() , (II-61)
, (II-61)
unde ω reprezintǎ pulsatia sursei de
alimentare, iar θ - faza initialǎ a tensiunii u(t), in regim
cvasistationar, in raport cu pozitia medianǎ a armǎturii mobile (care
vibreazǎ), Yo si respectiv in raport cu fluxul magnetic total
de pulsatie ω, ![]() , sistemul de ecuatii (I-55) se poate scrie:
, sistemul de ecuatii (I-55) se poate scrie:
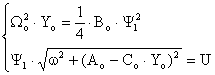 , (II-62)
, (II-62)
astfel incat, apeland la relatiile evidente:
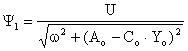 ,
, ![]() ,
, ![]() , (II-63)
, (II-63)
pozitia yo = Yo/(δo+a)<1 a armǎturii mobile a electromagnetului considerat, rezultǎ ca solutie a ecuatiei:
![]() , (II-64)
, (II-64)
unde:
![]() si
si ![]() . (II-65)
. (II-65)
Dacǎ se considerǎ acum curbele corespunzǎtoare functiilor f1(yo, β), avand forma prezentatǎ in Fig. II-16, care permit identificarea pozitiilor posibile ale armǎturii mobile a electromagnetului, prin punctele de intersectie cu paralelele la axa absciselor de ecuatie g1(U, yo), de ordonatǎ definitǎ prin valorile amplitudinii U a tensiunii de alimentare a circuitului bobinei, cu U1<U2<U3< <Un, se pot identifica tensiunea de actionare Ua= U3, pentru care se realizeazǎ saltul crescǎtor al valorilor yo (deci "actionarea"), si respectiv tensiunea de revenire, Ur, pentru care se obtine saltul scǎzǎtor al valorilor yo, (deci "revenirea"). Valoarea maximǎ posibilǎ a deplasǎrii raportate a armǎturii mobile este evident yo max =(δo / δo+a)<1.
Semnalǎm faptul cǎ graficul functiei f1(yo, β) are alura datǎ in Fig. II-16, atunci cand derivata acesteia, f1'(yo,β) are rǎdǎcini reale, deci pentru:
![]() , sau
, sau ![]() , cu
, cu ![]() . (II-66)
. (II-66)
In aceste conditii se poate chiar defini tensiunea de actionare sigurǎ pentru electromagnetii de c.a. cu FPN, Ua, datǎ de relatia:
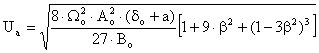 , (II-67)
, (II-67)
care evidentiazǎ si influenta diferitilor factori asupra procesului de "actionare" al acestora.
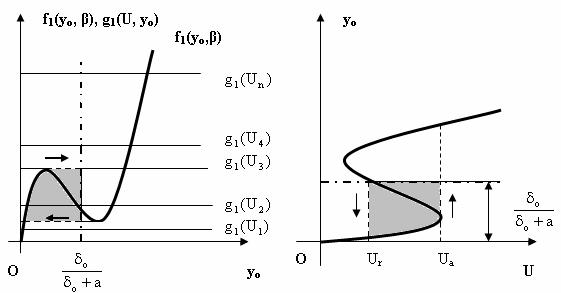
Fig. II-16 : Caracteristica de tip "releu" pentru electromagneti de c.a. cu FPN
Pentru situatia in care rǎdǎcinile ecuatiei:
f1'(yo, β) = 0 (II-68)
sunt complex conjugate, deci pentru valori
β > ![]() , curba f1(yo, β) nu mai
prezintǎ puncte de extrem si deci pozitia armǎturii mobile a
electromagnetului considerat, urmǎreste continuu, intr-o primǎ
aproximatie, valorile amplitudinii tensiunii de alimentare a circuitului
bobinei, U.
, curba f1(yo, β) nu mai
prezintǎ puncte de extrem si deci pozitia armǎturii mobile a
electromagnetului considerat, urmǎreste continuu, intr-o primǎ
aproximatie, valorile amplitudinii tensiunii de alimentare a circuitului
bobinei, U.
Dacǎ se comparǎ functionarea electromagnetilor cu FPN in curent continuu si respectiv in curent alternativ, v. Fig. II-14, II-15 si II-16, se constatǎ cǎ la functionarea in c.a. valorile tensiunii de revenire, Ur, sunt mai apropiate de valorile tensiunii de actionare, Ua, deci functionarea unor asemenea electromagneti in regim de releu este mai performantǎ in c.a.
3. 3. Forta de atractie la electromagnetii de curent continuu. Factori de influentǎ
Functionarea electromagnetilor are la bazǎ conversia energiei electrice, a sursei de alimentare a circuitului bobinei, in energie mecanicǎ, care se manifestǎ prin forte, F, sau cupluri, M, ce fac posibile deplasǎri predeterminate utile ale armǎturii lor mobile.
Este important deci sǎ evaluǎm aceste actiuni mecanice la nivelul armǎturii mobile si sǎ identificǎm factorii de influentǎ ce intervin, in scopul realizǎrii unor electromagneti cat mai performanti si cat mai bine adaptati unor aplicatii date.
Pentru
evaluarea fortei de atractie dintre douǎ piese polare de suprafatǎ S
(cu versorul ![]() corespunzǎtor
elementului de suprafatǎ infinitezimalǎ dS), prin care se inchid
linii de camp magnetic de inductie magneticǎ
corespunzǎtor
elementului de suprafatǎ infinitezimalǎ dS), prin care se inchid
linii de camp magnetic de inductie magneticǎ ![]() , se apeleazǎ la relatia lui Maxwell:
, se apeleazǎ la relatia lui Maxwell:
![]() , (II-69)
, (II-69)
care, in cazul unei perechi de piese polare
plan-paralele, cum intalnim adesea in practicǎ, v. Fig. II-17, cand ![]() , se scrie sub forma:
, se scrie sub forma:
![]() , cu
, cu ![]() . (II-70)
. (II-70)
![]()
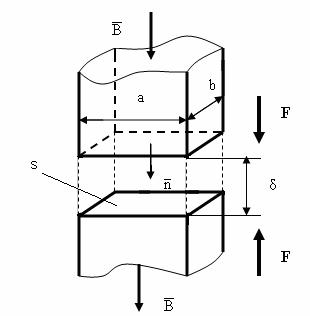
Fig. II-17 : Cu privire la forta de atractie la electromagneti
Relatia anterioarǎ nu pune in evidentǎ influenta intrefierului δ, influenta geometriei miezului magnetic si nici influenta curentului ce parcurge spirele bobinei (a solenatiei), asupra fortei de atractie (a cuplului de atractie), astfel incat adesea sunt preferate expresii mai explicite ale dependentei acestora in functie de diferiti parametri, care se deduc dacǎ se considerǎ fortele generalizate la nivelul intrefierurilor de lucru, Fx:
![]() , (II-71)
, (II-71)
unde Wmagn reprezintǎ energia campului magnetic, localizatǎ in principal la nivelul intrefierurilor, iar x - coordonata generalizatǎ, deplasare liniarǎ cand Fx este o fortǎ mecanicǎ, respectiv o deplasare unghiularǎ, cand forta generalizatǎ este un cuplu mecanic.
Corespunzǎtor cazului anterior, referitor la o pereche de piese polare plan-paralele, v. Fig. II-17, energia campului magnetic, Wmagn, se poate evalua cu ajutorul relatiei:
![]() , cu
, cu ![]() ,
, ![]() , (II-72)
, (II-72)
cu considerarea semnificatiilor mǎrimilor ce intervin ce rezultǎ din expresiile (II-2) si (II-3), astfel incat, folosind relatia (II-71), se evidentiazǎ practic dependenta fortei de atractie de valorile intrefierului, F(δ), care reprezintǎ caracteristica electromecanicǎ a electromagnetilor:
![]() . (II-73)
. (II-73)
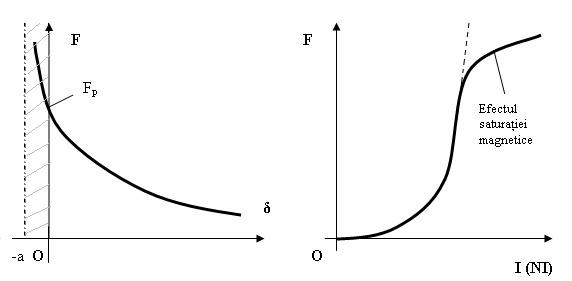
Alura caracteristicii electromecanice pentru un electromagnet de tip U-I este indicatǎ in Fig. II-18a, in care se precizeazǎ si forta portantǎ, Fp, de valoare finitǎ pentru intrefier nul, in timp ce dependenta fortei de atractie de valorile curentului I, ce parcurge spirele bobinei, este precizatǎ in Fig. II-18b, cu considerarea efectelor saturatiei miezului feromagnetic.
a) b)
Fig. II-18 : Factori de influentǎ asupra fortei de atractie la electromagneti
Dacǎ pentru acelasi electromagnet de tip U-I se scrie expresia energiei campului magnetic sub forma:
![]() , (II-74)
, (II-74)
unde permeanta intrefierului, ![]() se calculeazǎ cu
ajutorul relatiei, v. Fig. II-17:
se calculeazǎ cu
ajutorul relatiei, v. Fig. II-17:
![]() , (II-75)
, (II-75)
se obtine final :
![]() , (II-76)
, (II-76)
expresie desigur mai putin precisǎ dar care este acceptatǎ adesea, care indicǎ valori infinite ale fortei portante a electromagnetilor pentru valori nule ale intrefierului, ceea ce nu este in concordantǎ cu realitatea. Vom prefera deci o relatie mai riguroasǎ, de forma (II-73).
Un alt factor de influentǎ asupra fortei de atractie dezvoltate de electromagneti, il reprezintǎ geometria miezului feromagnetic. Pentru a pune in evidentǎ o asemenea influentǎ, vom preciza expresia fortei de atractie, pentru cateva forme uzuale de miezurilor feromagnetice in zona intrefierurilor de lucru.
In
cazul unui intrefier cilindric, obtinut intre un cilindru exterior de
diametru D si un cilindru interior (armǎturǎ mobilǎ) de diametru
d, v. Fig. II-19, permeanta intrefierului, ![]() se poate calcula cu ajutorul
uneia dintre relatiile:
se poate calcula cu ajutorul
uneia dintre relatiile:
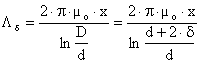 sau
sau 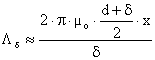 , (II-77)
, (II-77)
obtinandu-se forta Fx datǎ de expresiile:
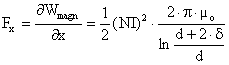 sau
sau 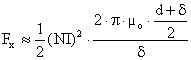 , (II-78)
, (II-78)
unde s-a considerat expresia (II-74) a energiei campului magnetic.
![]()
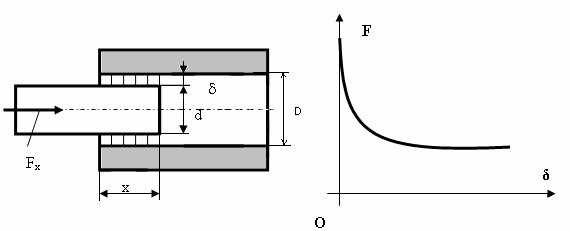
Fig. II-19 : Forta de atractie pentru electromagneti cu intrefier cilindric
Se constatǎ cǎ in cazul acestor electromagneti, de tip plonjor, caracteristica electromecanicǎ F(δ) prezintǎ o plaja largǎ de valori ale intrefierului pentru care forta de atractie rǎmane practic constantǎ.
In cazu electromagnetilor de tip plonjor cu circuit magnetic deschis, cum este cel prezentat in Fig. II-20, forta de atractie prezintǎ un maximul pentru armǎtura mobilǎ plasatǎ in mijlocul bobinei.
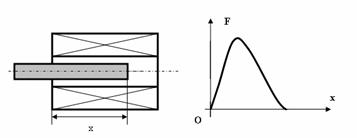
Fig. II-20 : Forta de atractie pentru electromagneti plonjor cu circuit magnetic deschis
In
cazul unui electromagnet cu intrefier conic sau tronconic, cum este cel
prezentat in Fig. II-21, acceptand notatiile din figurǎ, permeanta
intrefierului ![]() , se poate calcula cu ajutorul relatiei:
, se poate calcula cu ajutorul relatiei:
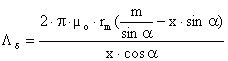 , cu
, cu ![]() , (II-79)
, (II-79)
unde r2 este raza micǎ a trunchiului de con, astfel incat, considerand relatiile (II-71) si (II-74) se obtine:
![]() , (II-80)
, (II-80)
2r2
cu valori maxime ale acestei forte pentru α
= 0, deci pentru fete plan-paralele, configuratia tronconicǎ atenuand
influenta cresterii intrefierului.
Fig. II-21 : Intrefier tronconic Fig. II-22 : Armǎturǎ mobilǎ de rotatie
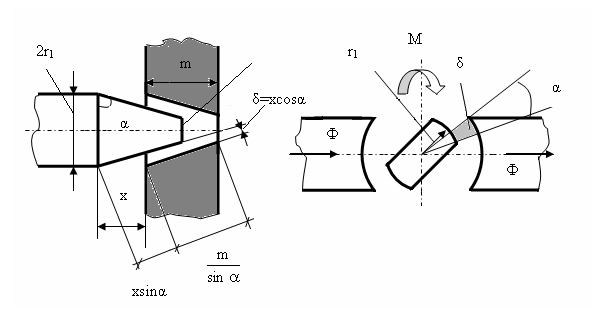
In
cazul unui electromagnet cu miscare de rotatie a armǎturii mobile, cum
este cel prezentat in Fig. II-22, cuplul mecanic M, care tinde sǎ
roteascǎ armǎtura mobilǎ in sensul sǎgetii, se defineste
tot ca fortǎ generalizatǎ de tip Lagrange, in raport cu coordonata
generalizatǎ ![]() care este unghiul de
rotatie al armǎturii mobile:
care este unghiul de
rotatie al armǎturii mobile:
![]() , (II-81)
, (II-81)
cu permeanta intrefierului datǎ de relatia:
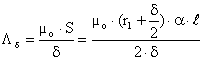 , (II-82)
, (II-82)
astfel incat tinand seama de expresia (II-74)
a energiei campului magnetic, pentru lungimea ![]() a miezului (a
intrefierului), rezultǎ final:
a miezului (a
intrefierului), rezultǎ final:
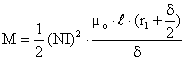 . (II-83)
. (II-83)
Este evident cǎ valorile momentului M cresc la scǎderea valorilor intrefierului δ, ceea ce se confirmǎ si ca o preocupare fireascǎ pentru constructiile performante de masini electrice.
Mentionǎm cǎ influenta geometriei miezului feromagnetic asupra fortei de atractie pentru electromagneti, sugeratǎ de cele prezentate mai sus, este completatǎ de faptul cǎ pozitia bobinei electromagnetului in raport cu intrefierul poate favoriza obtinerea unor forte de atractie mai mari, dacǎ aceasta este mai aproape de intrefierul de lucru.
Putem afirma cǎ actiunea mecanicǎ asupra armǎturii mobile a electromagnetilor este influentatǎ de o multitudine de factori, a cǎror cunoastere permite realizarea unor constructii performante pentru asemenea dispozitive.
3. 4. Forta de atractie la electromagnetii de curent alternativ
In cazul
electromagnetilor de curent alternativ, curentul care parcurge spirele bobinei
are o evolutie armonicǎ (sinusoidalǎ de exemplu), la fel ca si
inductia magneticǎ sau fluxul magnetic din miez. Considerand relatiile
(II-70), (II-73) sau (II-76), ce definesc forta de atractie care
actioneazǎ asupra armǎturii lor mobile, ce depinde de pǎtratul
curentului I, (pǎtratul solenatiei), sau de pǎtratul inductiei
magnetice B/pǎtratul fluxului magnetic ![]() , vom putea scrie, pentru o pozitie datǎ a
armǎturii mobile (considerǎm obisnuit situatia "actionat"), relatii
de forma:
, vom putea scrie, pentru o pozitie datǎ a
armǎturii mobile (considerǎm obisnuit situatia "actionat"), relatii
de forma:
![]() ,
, ![]() , (II-84)
, (II-84)
cu ![]() , sau:
, sau:
![]() ,
, ![]() , (II-85)
, (II-85)
respectiv, pentru ![]() :
:
![]() ,
, ![]() . (II-86)
. (II-86)
Se constatǎ cǎ forta de atractie care se exercitǎ asupra armǎturii mobile a unui electromagnet de curent alternativ, F(t), se modificǎ cu pulsatie dublǎ fatǎ de aceea a sursei de alimentare a circuitului bobinei, deci nu depinde de polaritatea curentului (a inductiei magnetice sau a fluxului magnetic), asa cum se poate observa in Fig. II-23.
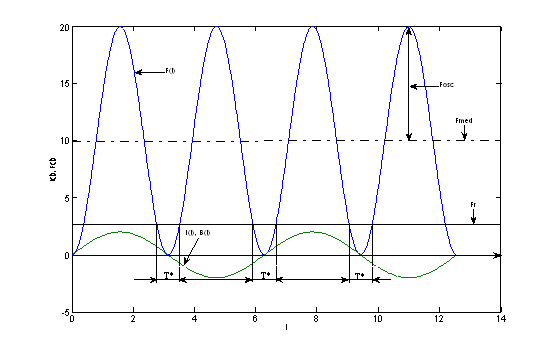
Fig. II-23 : Forta de atractie pentru electromagnetii de curent alternativ
Expresiile (II-84), (II-85) si (II-86), corespunzǎtoare evolutiei in timp a fortei de atractie pentru electromagnetii de curent alternativ, pun in evidentǎ o valoare medie, Fmed, egalǎ practic cu componenta oscilantǎ a fortei lor de atractie, Fosc, care sunt definite de relatiile:
![]() , (II-87)
, (II-87)
astfel incat valoarea minimǎ a fortei de atractie pentru asemenea electromagneti va fi nulǎ:
![]() . (II-88)
. (II-88)
Tinand
seama de faptul cǎ functionarea unui dispozitiv electromagnetic presupune
dezvoltarea unor forte active cu valori superioare fortelor rezistente, FR
din Fig. II-23, rezultǎ faptul cǎ existǎ intervale de timp ![]() , in care armǎtura mobilǎ are tendinta de a se
desprinde de piesele fixe ale miezului feromagnetic, dupǎ care va fi din
nou atrasǎ de miez, putandu-se manifesta deci vibratii ale armǎturii
mobile a electromagnetilor de curent alternativ, de frecventǎ audio,
dublǎ fatǎ de aceea a sursei de alimentare a circuitului bobinei.
, in care armǎtura mobilǎ are tendinta de a se
desprinde de piesele fixe ale miezului feromagnetic, dupǎ care va fi din
nou atrasǎ de miez, putandu-se manifesta deci vibratii ale armǎturii
mobile a electromagnetilor de curent alternativ, de frecventǎ audio,
dublǎ fatǎ de aceea a sursei de alimentare a circuitului bobinei.
Trebuie remarcat de asemenea faptul cǎ, valoarea efectivǎ a curentului care parcurge spirele bobinei unui electromagnet de curent alternativ, I, este definitǎ de raportul dintre valoarea efectivǎ a tensiunii de alimentare a bobinei, U, si valoarea impedantei infǎsurǎrii, Z, rezultand succesiv:
![]() , (II-89)
, (II-89)
unde s-a tinut seama de relatia (II-2) si de
faptul cǎ pentru asemenea electromagneti , ![]() , L fiind inductivitatea bobinei, iar R-rezistenta acesteia,
astfel incat putem afirma cǎ valorile curentului I, sunt practic
proportionale cu intrefierul δ.
, L fiind inductivitatea bobinei, iar R-rezistenta acesteia,
astfel incat putem afirma cǎ valorile curentului I, sunt practic
proportionale cu intrefierul δ.
Analizand acum expresia (II-84) a fortei de atractie F(t), pentru un electromagnet monofazat de tip U-I de curent alternativ, ale cǎrei valori depind de pǎtratul solenatiei (NI)2, dar si de pǎtratul intrefierului, δ2:
![]() , (II-90)
, (II-90)
ceea ce sugereazǎ faptul cǎ in cazul electromagnetilor de curent alternativ influenta valorilor intrefierului asupra valorilor fortei de atractie este mai redusǎ, caracteristica electromecanicǎ F(δ) fiind mai putin cǎzǎtoare decat in cazul electromagnetilor de curent continuu.
Comparand caracteristica Fcc(δ) corespunzǎtoare functionǎrii in curent continuu, pentru un electromagnet de tip U-I de exemplu, cu caracteristica Fca(δ) corespunzǎtoare aceluiasi electromagnet la functionarea in curent alternativ (pentru valorile medii ale fortei), v. Fig. II-24, se constatǎ cǎ la alimentarea circuitului bobinei in curent alternativ functionarea poate decurge la valori mai mari ale intrefierului, pentru o fortǎ rezistentǎ FR datǎ, desi forta portantǎ in curent alternativ este doar jumǎtate din valoarea acesteia la functionarea in curent continuu, in conditiile in care bobina realizeazǎ aceeasi solenatie in ambele situatii.
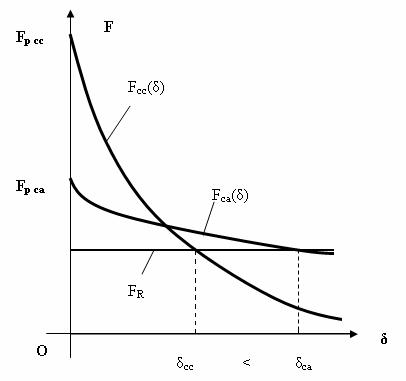
Fig. II-24 : Caracteristica electromecanicǎ pentru electromagnetii de curent alternativ
Se poate deci afirma cǎ forta de atractie care actioneazǎ asupra armǎturii mobile a electromagnetilor de curent alternativ, se modificǎ in timp cu frecventǎ dublǎ fatǎ de aceea a tensiunii de alimentare a circuitului bobinei, asigurand o fortǎ portantǎ egalǎ cu jumǎtate din valoarea obtinutǎ pentru acelasi miez, functionand cu aceeasi solenatie, dar in curent continuu, insǎ caracteristica electromecanicǎ este mai putin cǎzǎtoare si in consecintǎ intrefierul initial (de lucru), poate fi mai mare in cazul alimentǎrii circuitului bobinei in curent alternativ.
3. 5. Problema vibratiei armǎturii mobile la electromagnetii de c.a.
Anuntǎm de la inceput faptul cǎ problema vibratiei armǎturii mobile se pune diferit pentru electromagnetii monofazati fatǎ de electromagnetii trifazati de curent alternativ.
Dupǎ cum s-a arǎtat mai sus, v. Fig. II-23, forta de atractie care actioneazǎ asupra armǎturii mobile a electromagnetilor monofazati de curent alternativ este variabilǎ in timp, astfel incat evidentiazǎ intervale foarte scurte de timp in care aceasta este mai micǎ decat forta rezistentǎ, ceea ce conduce la tendinta de desprindere a armǎturii mobile, urmatǎ imediat de reatragerea acesteia, fǎcand posibile vibratii ale armǎturii mobile a electromagnetilor monofazati, cu frecventa dublǎ fatǎ de aceea a sursei de alimentare a circuitului bobinei.
FR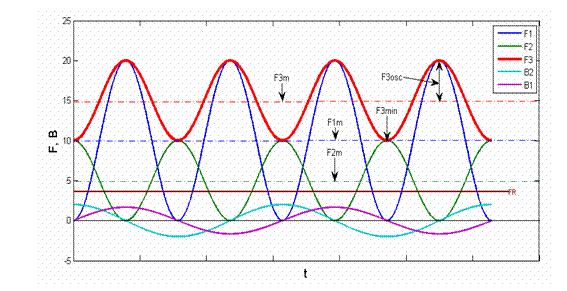 Solutia pentru
eliminarea acestor vibratii, v. Fig. II-25, este aceea de a asigura actiunea
localǎ, in zona intrefierului, a douǎ fluxuri magnetice, defazate cu
unghiul θ intre ele,
Solutia pentru
eliminarea acestor vibratii, v. Fig. II-25, este aceea de a asigura actiunea
localǎ, in zona intrefierului, a douǎ fluxuri magnetice, defazate cu
unghiul θ intre ele, ![]() si
si ![]() , respectiv interventia inductiilor magnetice B1(t)
si B2(t), astfel incat, prin compunerea fortelor de atractie
corespunzǎtoare, F1(t) si F2(t), forta
rezultantǎ F3(t), prezintǎ valori minime nenule, mai mari
decat forta rezistentǎ, FR, evitandu-se astfel asemenea
manifestǎri.
, respectiv interventia inductiilor magnetice B1(t)
si B2(t), astfel incat, prin compunerea fortelor de atractie
corespunzǎtoare, F1(t) si F2(t), forta
rezultantǎ F3(t), prezintǎ valori minime nenule, mai mari
decat forta rezistentǎ, FR, evitandu-se astfel asemenea
manifestǎri.
Fig. II-25 : Cu privire la eliminarea vibratiilor armǎturii mobile a electromagnetilor de c.a.
Pentru obtinerea celor douǎ fluxuri magnetice defazate se pot folosi douǎ miezuri care actioneazǎ asupra aceleiasi armǎturi mobile, cu douǎ bobine alimentate de la douǎ surse de tensiune defazate intre ele, ca in Fig. II-26a, sau se poate diviza miezul in zona pieselor polare, cu amplasarea in zonǎ a douǎ infǎsurǎri care genereazǎ fluxurile defazate, deoarece una dintre acestea este conectatǎ la sursa de tensiune printr-un condensator, v. Fig. II-26b.
Dacǎ se acceptǎ cǎ fluxurile magnetice generate de cele douǎ bobine sunt egale ca amplitudine, dar defazate intre ele cu unghiul α:
![]() ,
, ![]() , (II-91)
, (II-91)
atunci, pentru circuite magnetice identice, fortele de atractie F1 si F2 vor fi:
![]() ,
, ![]() , (II-92)
, (II-92)
iar forta de atractie rezultantǎ, F(t), se scrie:
![]() , (II-93)
, (II-93)
evidentiind o valoare medie, Fmed si o valoare oscilantǎ, Fosc :
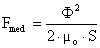 ,
, ![]() , (II-94)
, (II-94)
astfel incat vibratiile armǎturii mobile sunt eliminate, dacǎ forta minimǎ de atractie, Fmin, nenulǎ, depǎseste valarea fortei rezistente maxime, FR:
![]() , (II-95)
, (II-95)
conditie satisfǎcutǎ pentru valori cosα de dorit cat mai mici.
Cea mai simplǎ solutie pentru a obtine actiunea localǎ, in zona pieselor polare, a douǎ fluxuri magnetice defazate, apeleazǎ la spire in scurtcircuit (sau spire ecran), care, asa cum sugereazǎ denumirea lor, ecraneazǎ partial piesele polare si asigurǎ eliminarea vibratiilor armǎturii mobile, pentru electromagneti realizati cu un singur circuit magnetic, cu o singurǎ bobinǎ si cu o singurǎ sursǎ de alimentare a acesteia, solutie care este preferatǎ, si unanim acceptatǎ, de producǎtorii de electromagneti din intreaga lume.
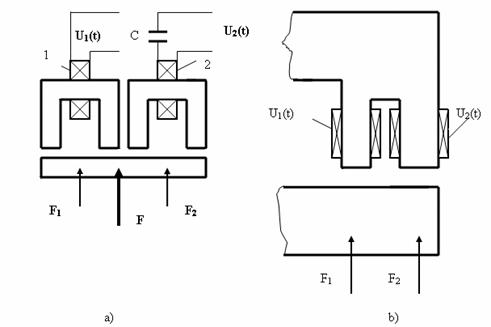
Fig. II-26 : Posibilitǎti de eliminare a vibratiilor pentru electromagnetii monofazati
Amplasarea spirelor in scurt-circuit pentru o pereche de piese polare ale unui electromagnet de curent alternativ este indicatǎ in Fig. II-27.
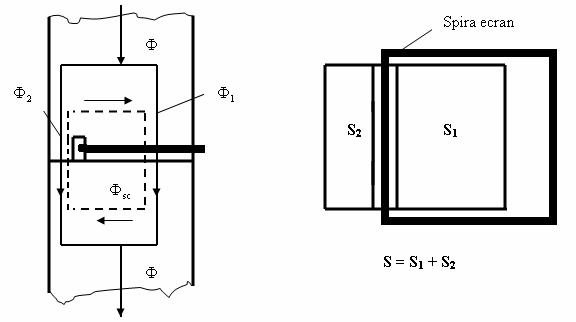
Fig. II-27 : Amplasarea spirei in scurtcircuit pe o pereche de piese polare
Considerand
o distributie uniformǎ a campului pagnetic in sectiunea transversalǎ
a miezului feromagnetic, cu neglijarea fluxurilor de dispersie justificatǎ
in cazul unor piese polare rectificate, cu contacte megnetice de calitate, se
poate accepta cǎ amplitudinile fluxurilor magnetice ![]() si
si ![]() , corespunzǎtoare suprafetelor S1 si
respectiv S2, vor fi proportionale cu aceste suprafete, v. Fig.
II-27, putand deci scrie succesiv:
, corespunzǎtoare suprafetelor S1 si
respectiv S2, vor fi proportionale cu aceste suprafete, v. Fig.
II-27, putand deci scrie succesiv:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , (II-96)
, (II-96)
sau, final:
![]() . (II-97)
. (II-97)
Datoritǎ
interventiei locale a spirei ecran, in zona pieselor polare, se manifestǎ
un flux produs de aceasta, ![]() , astfel incat, acceptand fazorii corespunzǎtori,
fluxurile magnetice rezultante in zona ecranatǎ si respectiv in zona
neecranatǎ,
, astfel incat, acceptand fazorii corespunzǎtori,
fluxurile magnetice rezultante in zona ecranatǎ si respectiv in zona
neecranatǎ, ![]() , respectiv
, respectiv ![]() vor fi:
vor fi:
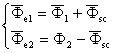 , (II-98)
, (II-98)
in care fluxul ![]() este desigur cel care
genereazǎ fluxul
este desigur cel care
genereazǎ fluxul ![]() , prin tensiunea
, prin tensiunea ![]() indusǎ in spira
ecran, care este astfel parcursǎ de curentul
indusǎ in spira
ecran, care este astfel parcursǎ de curentul ![]() , limitat de impedanta
, limitat de impedanta ![]() a spirei ecran, de
rezistentǎ Rsc si de inductantǎ Lsc:
a spirei ecran, de
rezistentǎ Rsc si de inductantǎ Lsc:
![]() ,
, ![]() ,
, ![]() ,
, ![]() . (II-99)
. (II-99)
Tinand
seama de relatiile (II-97), (II-98) si (II-99), expresiile, in complex, pentru
fluxurile magnetice ![]() si
si ![]() se pot scrie sub
forma:
se pot scrie sub
forma:
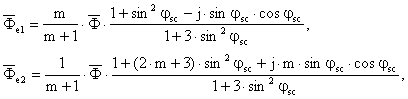 (II-100)
(II-100)
care permit apoi definirea modulelor acestora:
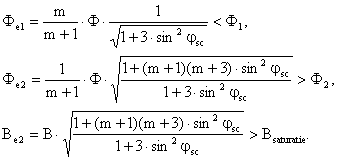 (II-101)
(II-101)
Corespunzǎtor
fazorilor ![]() si
si ![]() , se poate evalua unghiul de defazaj dintre aceste fluxuri
magnetice, θ:
, se poate evalua unghiul de defazaj dintre aceste fluxuri
magnetice, θ:
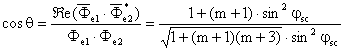 , (II-102)
, (II-102)
relatia de mai sus anuntand deja posibile
puncte de extrem, interesante pentru proiectarea optimalǎ a unor asemenea
electromagneti, atat din punct de vedere al valorilor "![]() ", (cu cosθ=1 pentru x=0, dar si pentru x=1), cat si din
punct de dedere al valorilor raportului "m", dintre aria ecranatǎ si aria
neecranatǎ a pieselor polare (vezi valorile cosθ pentru m tinzand
cǎtre zero si respectiv cǎtre infinit, unghiul θ crescand pentru
valori
", (cu cosθ=1 pentru x=0, dar si pentru x=1), cat si din
punct de dedere al valorilor raportului "m", dintre aria ecranatǎ si aria
neecranatǎ a pieselor polare (vezi valorile cosθ pentru m tinzand
cǎtre zero si respectiv cǎtre infinit, unghiul θ crescand pentru
valori ![]() scǎzǎtoare).
scǎzǎtoare).
Diagrama
fazorialǎ asociatǎ functionǎrii spirei ecran pentru
electromagnetii monofazati, este indicatǎ in Fig. II-28 si indicǎ
tendinta de saturatie magneticǎ a zonei neecranate a pieselor polare (![]() ).
).
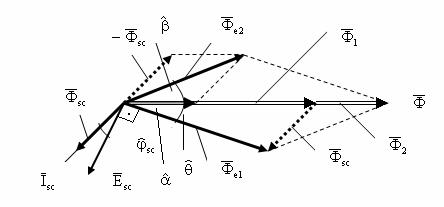
Fig. II-28 : Diagrama fazorialǎ cu privire la functionarea spirei ecran
Fluxurile
magnetice rezultante in zona ecranatǎ, respectiv in zona neecranatǎ a
pieselor polare, ![]() si
si ![]() , generea zǎ
componente medii si oscilante ale fortei de atractie, astfel:
, generea zǎ
componente medii si oscilante ale fortei de atractie, astfel:
![]() ,
, ![]() , (II-103)
, (II-103)
astfel incat componentele, medie respectiv
oscilantǎ, ale fortei rezultante de atractie Fmed si Fosc,
vor fi, (x =![]() ):
):
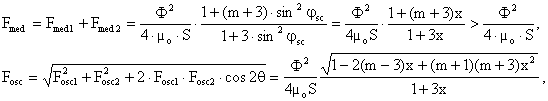 (II-104)
(II-104)
pentru forta minimǎ de atractie obtinandu-se final:
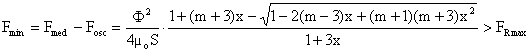 , (II-105)
, (II-105)
inegalitatea finalǎ fiind tocmai conditia de eliminare a vibratiilor armǎturii mobile.
Amplasarea spirelor in scurtcircuit pentru diferite tipuri de miezuri feromagnetice, tipice pentru electromagnetii monofazati, este ilustratǎ in Fig. II-29.
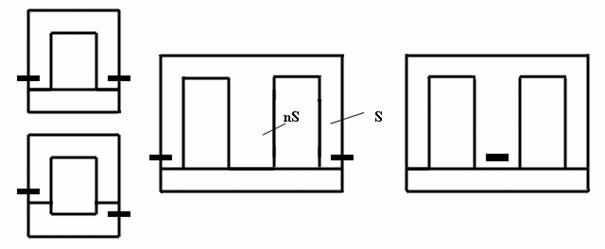
Fig. II-29 : Amplasarea spirelor ecran pentru electromagnetii monofazati
Se constatǎ cǎ electromagnetii de tip E-I pot functiona cu o singurǎ spirǎ ecran, plasatǎ pe coloana medianǎ de sectiune transversalǎ nS, sau cu douǎ spire ecran, plasate pe coloanele laterale, de sectiune transversalǎ S, cu observatia cǎ cele douǎ situatii sunt echivalente ca performante pentru cazul in care sectinea coloanei mediane este dublǎ fatǎ de aceea a coloanelor laterale (n=2), cand se obtin aceleasi valori pentru componentele medie si oscilantǎ ale fortei rezultante, deci si aceeasi valoare a fortei minime. Optiunea pentru o solutie constructivǎ sau altǎ considerǎ in principal incǎlzirea bobinei acestor electromagneti (cu utilizarea fie a douǎ semibobine, conectate in serie si amplasate pe coloanele laterale, fie doar a unei singure bobine, plasate pe coloana medianǎ).
Procedand deci la un calcul similar cu cel anterior, referitor la o pereche de piese polare ale unui electromagnet monifazat de tip U-I, pentru electromagnetii monofazati de tip E-I, realizati cu sectiunea transversalǎ a coloanei mediane de douǎ ori mai mare decat aceea a coloanelor laterale, se obtine final:
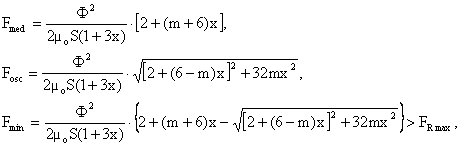 (II-106)
(II-106)
ultima inegalitate corespunzand conditiei de eliminare a vibratiilor armǎturii mobile pentru asemenea electromagneti.
Considerand relatia (II-1013), ce confirmǎ tendinta de saturare magneticǎ a zonei neecranate a piesei polare a unui electromagnet cu spirǎ in scurtcircuit, pentru care amplitudinea inductiei magnetice este limitatǎ la un domeniu restrans, Be2 = (2-2,4) [T], si apeland la expresiile (II-105), respectiv (II-106) ale fortei minime de atractie pentru electromagneti de tip U-I sau de tip E-I, se pot defini conditii de functionare optimǎ a unor asemenea ansambluri electromagnet-spirǎ ecran, ca solutie a unui sistem de ecuatii de forma:
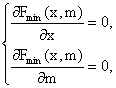 (II-107)
(II-107)
care presupun realizarea "acordului" optim intre parameterii spirelor in scurtcircuit si raportul m (arie ecranatǎ/arie neecranatǎ a pieselor polare).
Rezolvand ecuatiile corespunzǎtoare pentru cazul electromagnetilor de tip U-I cu spire ecran se obtine conditia de functionare optimǎ a acestora, []:
m
= 4 , ![]() , (II-108)
, (II-108)
ce corespunde unor valori maxime ale fortei minime de atractie, deci unor valori minime ale sectiunii transversale din fier, pentru o fortǎ rezistentǎ datǎ, in cazul proiectǎrii.
Pentru electromagnetii de tip E-I cu spire ecran, procedand similar, conditia de functionare optimǎ corespunde unor valori, []:
m
= 4 , ![]() , (II-109)
, (II-109)
care se refarǎ la situatia in care coloana medianǎ a miezului are sectiunea transversalǎ dublǎ fatǎ de coloanele laterale, indiferent dacǎ se foloseste o singurǎ spirǎ ecran sau douǎ.
In
cazul electromagnetilor trifazati de curent alternativ, care se
realizeazǎ de obicei cu circuite magnetice E-I sau E-E, v. Fig. II-30,
pentru fiecare dintre fazele sursei de
alimentare extstǎ cate o bobinǎ, amplasatǎ pe una dintre
coloanele miezului feromagnetic, cele trei bobine, identice, generand firesc
trei fluxuri magnetice defazate intre ele cu (![]() ):
):
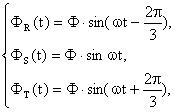 (II-110)
(II-110)
astfel incat, fǎrǎ a se utiliza spire ecran, expresiile fortelor de atractie ce actioneazǎ pe cele trei coloane de sectiune transversalǎ identicǎ, egala cu S, vor fi:
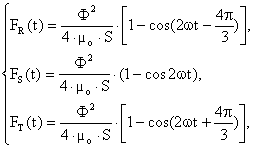 (II-111)
(II-111)
astfel incat forta rezultantǎ de atractie, F(t), va fi:
![]() , (II-112)
, (II-112)
deci constantǎ ca modul, dar cu punctul de aplicatie care se deplaseazǎ, dupǎ legea x(t), cu pulsatie dublǎ fatǎ de aceea a sursei de alimentare (2ω), cǎtre coloana corespunzǎtoare fortei de atractie cu valoare instantanee mai mare:
![]() , (II-113)
, (II-113)
unde ![]() este distanta dintre
axele coloanelor vecine ale miezului feromagnetic, v. Fig. II-30.
este distanta dintre
axele coloanelor vecine ale miezului feromagnetic, v. Fig. II-30.
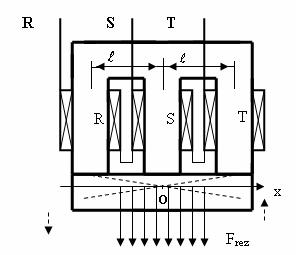
Fig. II-30 : Vibratia armǎturii mobile la electromagnetii trifazati
In aceste conditii, vibratia armǎturii mobile pentru electromagnetii trifazati se poate obtine doar ca o rotatie in jurul centrului de greutate al armǎturii lor mobile (O), in plan vertical, dacǎ coloana medianǎ reprezintǎ un punct de sprijin. Evitarea manifestǎrii acestor vibratii, presupune realizarea coloanei mediane cu circa 0,5 [mm] mai scurtǎ fatǎ de coloanele laterale, pe care se va sprijini deci armǎtura mobilǎ, fǎrǎ ca aceasta sǎ vibreze.
Eliminarea vibratiilor armǎturii mobile la electromagneti se obtine si prin alimentarea acestora cu tensiune redresatǎ, cand componentele oscilante, mai mici decat cele medii, permit obtinerea unor valori nenule ale fortei rezultante de atractie, superioare fortei rezistente maxime.
Trebuie semnalat faptul cǎ vibratiile armǎturii mobile a electromagnetilor de curent alternativ pot fi uneori utile, cum se intamplǎ in cazul realizǎrii vibratoarelor electromagnetice, care functioneazǎ de obicei unitact sau bitact, pe frecventa sursei de alimentare a bobinei, deci ca vibratoare sincrone, sau cu o frecventǎ dublǎ fatǎ de aceea a sursei de alimentare a circuitului bobinei, frecventa fiind inferioarǎ insǎ valorii de 100 [Hz]. Pentru a obtine functionarea cu o anumitǎ frecventǎ a vibratiilor, va trebui folositǎ o sursǎ de alimentare convenabilǎ. Se pot realiza de asemenea vibratoare electromagnetice de curent continuu, care functioneazǎ de obicei la frecvente mai scǎzute.
Pentru a obtine oscilatii mecanice de frecvente ridicate, se folosesc fie vibratoarele electrodinamice (f < 20.000 Hz), sau vibratoarele piezoelectrice, ce pot functiona chiar in domeniul ultrasunetelor.
3. Functionarea electromagnetilor in regim dinamic
4. Electromagneti polarizati
BIBLIOGRAFIE
Hnatiuc E., Sur le fonctionnement des électro-aimants monophasés à courant alternatif de type U-I ayant deux bagues de déphasage, Buletinul Institutului Politehnic din Iasi, Tom XXXVI(XL), Fasc. 1-2, Sectia a III-a, 1990
Hnatiuc E., Sur le calcul optimal des électro-aimants à courant alternatif de type U-I munis avec des bagues de déphasage, Buletinul Institutului Politehnic din Iasi, Tom XXXVII(XLI), Fasc. 1-4, Sectia a III-a, 1991
Hnatiuc E., Adam M., Sur une possibilité d'obtenir l'augmentation des performances des relais d'induction munis avec deux bagues de déphasage, Buletinul Institutului Politehnic din Iasi, Tom XXXVIII(XLII), Fasc. 1-4, Sectia a III-a, 1992
|
|