NOTIUNI DE ALGEBRA VECTORIALA

Marimi scalare - pot fi complet caracterizate printr-un scalar (un numar pozitiv sau negativ). (ex.:timpul, temperatura, lungimea).

Marimile vectoriale - sunt acele marimi caracterizate prin punct de aplicatie, directie, sens si marime.

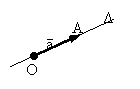
Vectorul este caracterizat prin ur matoarele elemente

punct de aplicatie sau originea O

suportul sau sau directia Δ;

sensul de parcurs de la O la A;

marimea vectorului sau modulul sau

(1.1)

Din punct de vedere al originii vectorilor, deosebim:

a.       Vectori liberi - a caror origine ocupa orice pozitie in spatiu, cu conditia pastrarii marimii, directiei si sensului (ex. viteza unui rigid in miscare de translatie)

b.  Vectori alunecatori - a caror origine poate ocupa orice pozitie pe suportul propriu, cu conditia pastrarii marimii si sensului (ex. forta ce actioneaza asupra unui rigid)

c.  Vectori legati - a caror origine ocupa un anumit loc in spatiu (o unica pozitie), (ex. forte ce actioneaza asupra unui punct material)

Vector echipotent - un vector liber avand directia paralela cu directia unui vector , acelasi sens si aceeasi marime cu vectorul

1. Vectorul Unitate

Fie ≠0 un vector liber. Numim versorul lui sau vectorul unitate, un vector , al carui suport este paralel cu suportul vectorului , are sensul lui si modulul egal cu unitatea:

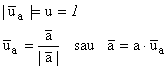(1.2)

2. Vector liber reprezentat Intr-o baza  ortonormata

Consideram triedrul triortogonal drept Oxzy si un vector liber (fig.1.2). - sunt versorii axelor Ox, Oz, Oy.

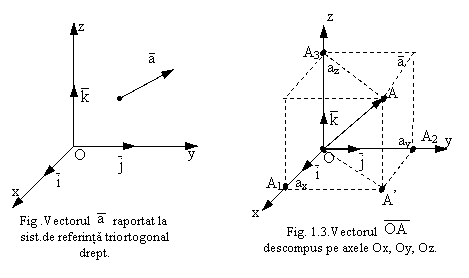
Componentele scalare ale vectorului pe axele Ox, Oy, Oz sunt: a_x, a_y, a_z.

Componentele vectoriale ale vectorului in sistemul Oxyz, sunt:

Reprezentarea vectorului in baza Oxyz, va fi:

(1.3)

Modulul vectorului

(1.4)

Cosinusii directori ai directiei vectorului

(1.5)

Daca:

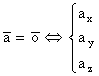(1.6)

In cazul vectorului (fig. 1.3), acesta se numeste vectorul de pozitie al punctului A:

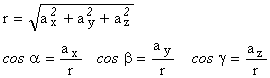(1.7)

3. Paralelismul si coplanaritatea vectorilor

Doi vectori sunt paraleli (au suporturile paralele), daca ( ) λ nenul astfel:

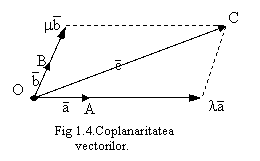
Trei vectori sunt coplanari daca ( ) simultan λ≠0, m≠0 astfel incat:

(1.9)

4. Operatii cu vectori

1. 2.4.1. Adunarea vectorilor

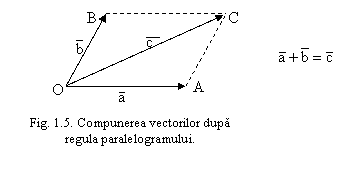
Suma a doi vectori este un vector care reprezinta diagonala paralelogramului construit cu cei doi vectori initiali (regula paralelogramului).

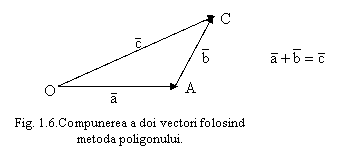
Regula poligonului: daca se construieste un vector echipolent vectorului , avand originea in varful vectorului , avand originea primului vector cu varful ultimului vector, obtinem vectorul rezultant (fig. 1.6).

Proprietatile adunarii vectorilor:

comutativitatea:

asociativitatea:

inmultirea unui vector cu un scalar m≠0:

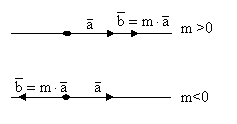
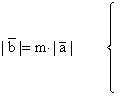
Produsul scalar a doi vectori

Fie vectorii si aplicati intr-un punct O (fig. 1.7).

Produsul scalar a doi vectori este scalarul:

               (1.10)

unde θ - unghiul dintre cei doi vectori

               (1.11)

Proprietatile produsului scalar:

comutativitatea: ;

distributivitate fata de suma: ;

) m,n =>: ;

produsul scalar a doi vectori identici:

produsul este nul daca: .

Expresia analitica a produsului scalar

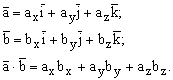(1.12)

Expresia versorului unui vector :

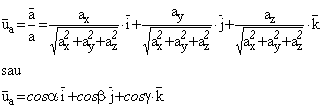(1.13)

Produsul vectorial a doi vectori

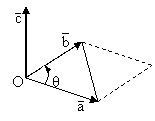Fiind dati doi vectori liberi reprezentati prin vectorii echivalenti, cu originea in O, produsul vectorial al celor doi vectori va fi un vector avand urmatoarele proprietati:

marimea:

;

directia: pe planul definit de vectorii ;

sensul: este sensul de inaintare al burghiului care se roteste in sensul suprapunerii primului vector peste cel de al doilea pe drumul cel mai scurt (regula burghiului).

Proprietatile produsului vectorial:

necomutativitatea: ;

asociativitatea la inmultirea cu scalari:

distributivitate fata de suma: ;

║.

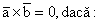
Expresia analitica a produsului vectorial:

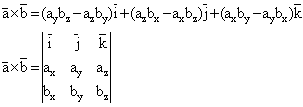(1.14)

Produsul mixt a trei vectori

Fie vectorii aplicati in punctul O.

Se defineste produsul mixt al celor trei vectori scalarul:

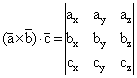                    (1.15)

Dublul produs vectorial a trei vectori

Fiind dati vectorii , definim produsul dublu vectorial al celor trei vectori, vectorul:

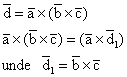(1.16)