STATICA RIGIDULUI

1. Echilibrul rigidului liber

Teorema: Conditia necesara si suficienta pentru ca un rigid liber sa ramana in repaus sub actiunea fortelor exterioare, este ca sistemul sa fie echivalent cu 0.

           (1.95)

Deoarece:

         (1.96)

Relatiile (1) devin:

                                (1.97)

Proiectiile pe axele unui sistem Oxyz, vor fi:

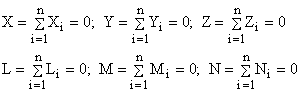                     (1.98)

Sisteme particulare de forte:

1. Asupra rigidului actioneaza un sistem de forte coplanare (in planul Oxy); ecuatiile scalare de echilibru se reduc la trei:

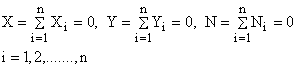                      (1.99)

2. Asupra rigidului actioneaza un sistem de forte paralele (cu axa Ox); ecuatiile scalare de echilibru se reduc la:

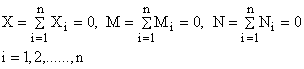(1.100)

3. Asupra rigidului actioneaza un sistem de forte coplanare si paralele (c u axa OX si planul Oxy); ecuatiile scalare de echilibru vor fi:

                   (1.101)

4. Asupra rigidului actioneaza un sistem de forte concurente (avand originea sistemului de axe in punctul de concurenta al fortelor); ecuatiile scalare de echilibru vor fi:

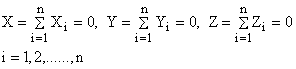    (1.102)

5. Asupra rigidului actioneaza un sistem de cupluri de forte; ecuatiile scalare de echilibru vor fi:

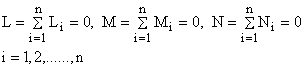                  (1.103)

Un rigid liber in spatiu are sase grade de libertate:

Ox: Translatie + Rotatie

Oy: Translatie + Rotatie

Oz: Translatie + Rotatie

Un rigid liber in plan are trei grade de libertate:

Ox: Translatie

Oy: Translatie

Oz: Rotatie

Problemele echilibrului rigidului liber sunt:

- se dau fortele care actioneaza asupra rigidului si se cere pozitia de echilibru a acestuia;

- se da pozitia de echilibru a rigidului si se cer fortele care actioneaza asupra acestuia la echilibru.

2. Rigidul supus la legaturi fara frecare

In cazul solidului rigid supus la legaturi, se aplica axioma legaturilor: legaturile se inlocuiesc cu forte si momente de legatura numite reactiuni.

Rigidul este liber, sub actiunea fortelor direct aplicate (cunoscute) si reactiunilor (necunoscute).

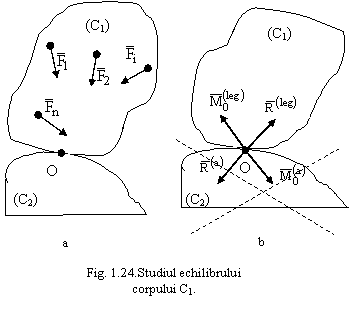
Fie doua corpuri C₁ si C₂, in contact intr-un punct O, (fig.1.24.a). Asupra corpului C₁ actioneaza fortele direct aplicate .

Pentru studiul echilibrului corpului C₁, conform axiomei legaturilor se inlatura corpul (C₂), se suprima legatura dintre C₁ si C₂, inlocuindu-se cu forte si cupluri de legatura (fig. 1.24.b).

Notatii:

- torsorul de reducere in O al fortelor exterioare date.

- torsorul de reducere in O al fortelor de legatura

Conditia de echilibru:

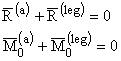(1.104)

Ecuatiile scalare de echilibru vor fi:

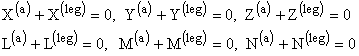
(1.105)

In cazul particular in care fortele apartin planului xOy, avem:

(1.106)

Legaturile micsoreaza numarul gradelor de libertate ale solidului rigid.

Legaturile ideale (fara frecare) ale rigidului sunt: reazemul simplu, articulatia, incastrarea, prinderea cu fire.

2.1. Reazemul simplu

Un rigid are un reazem simplu intr-un punct al sau, daca acest punct este obligat sa ramana pe o suprafata sau pe o curba. Suprafetele sau curbele sunt lucii, fixe si suficient de rezistente (nu se deformeaza sub actiunea fortelor din rigid).

Din punct de vedere geometric, reazemul simplu micsoreaza numarul gradelor de libertate ale rigidului cu o unitate; rigidul avand un reazem simplu are cinci grade de libertate.

Din punct de vedere mecanic, reazemul simplu se inlocuieste cu o reactiune , normala la suprafata de sprijin (e), (fig.1.25).

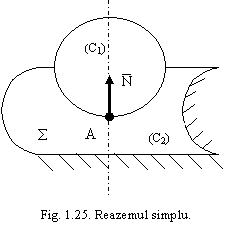
Atunci cand exista mai multe reazeme simple, fiecare dintre acestea se inlocuiesc cu o normala in punctul considerat pe suprafata de reazem respectiva.

2.2. Articulatia

Un rigid este articulat intr-un punct al sau, daca acesta este fix.

Articulatia poate fi spatiala (sferica) (pentru sisteme de forte in spatiu) sau plana, cilindrica (pentru sisteme de forte in plan).

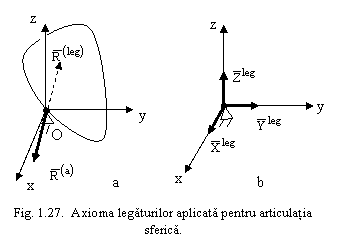
Articulatia sferica

Din punct de vedere geometric reduce numarul gradelor de libertate cu trei unitati.

Din punct de vedere mecanic - se inlocuieste cu o reactiune

de marime si directie necunoscute; aceasta se poate inlocui cu trei necunoscute scalare: X^leg, Y^leg, Z^leg - proiectiile pe directiile axelor sistemului Oxyz (fig.1.27a,b).

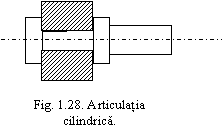
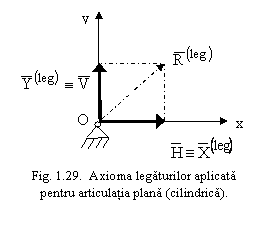
Din punct de vedere geometric - reduce numarul gradelor de libertate cu doua unitati

Din punct de vedere mecanic - legatura se inlocuieste cu o reactiune plana, de marime si directie necunoscute; aceasta se poate inlocui cu doua necunoscute scalare: X^leg, Y^leg (fig.1.29).

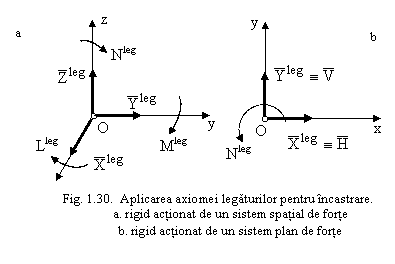
2.3. Incastrarea

Un rigid incastrat este un rigid complet fixat in raport cu un alt corp fix.

Din punct de vedere geometric - sunt reduse toate cele sase grade de libertate ale corpului.

Din punct de vedere mecanic - incastrarea se inlocuieste cu o reactiune (avand proiectiile X^leg, Y^leg, Z^leg pe axele sistemului

cartezian Oxyz) si un moment (avand proiectiile L^leg, M^leg, N^leg pe axele sistemului Oxyz).

3. Rigidul supus la legaturi cu frecare

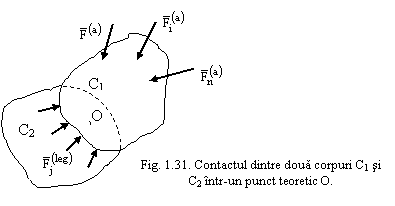
Consideram contactul dintre doua corpuri C₁ si C₂. Asupra corpului C₁ actioneaza forte exterioare direct aplicate . Corpul C₂ se deformeaza in realitate sub actiunea corpului C₁, astfel incat contactul se realizeaza pe o mica suprafata. In fiecare punct al suprafetei se dezvolta cate o reactiune , (fig. 1.31).

Aplicand axiaoma legaturilor si reducand sistemele de forte si in punctul O, rezulta conditiile vectoriale de echilibru (fig.1.32):

                    (1.107)

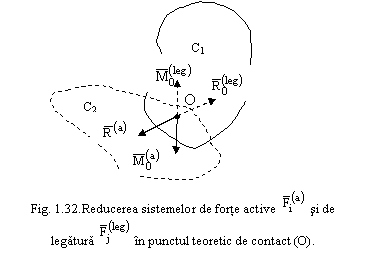
Vectorii din relatiile (1.107) se descompun dupa normala (On) planul tangent in O si dupa cate o directie din plan (Ot₁, Ot₂), obtinand relatiile:

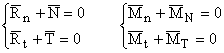                            (1.108)

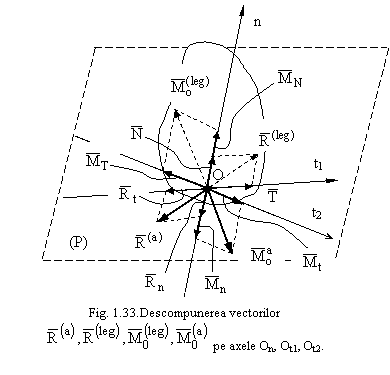
Efectele sarcinilor din relatiile (1.108) sunt:

Forta tinde sa deplaseze corpul in directia normala la suprafata de contact, deplasarea fiind insa impiedicata de reactiunea normala .

Forta tinde sa deplaseze corpul pe directia axei (O_t1), miscare suprimata de forta (forta de frecare de alunecare).

Momentul tinde sa roteasca corpul in jurul normalei la suprafata de contact, rotirea numindu-se pivotare si fiind impiedicata de momentul (cuplu de frecare de pivotare).

Momentul M_t tinde sa roteasca corpul in jurul unei axe (O_t2), rotire impiedicata de momentul (moment de frecare de rostogolire).

3.1. Frecarea de alunecare

Acest tip de frecare apare atunci cand torsorul de reducere al fortelor exterioare este format numai din rezultanta .

    (1.109)

Reactiunea planului () va fi conform principiului actiunii si reactiunii:

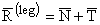                         (1.110)

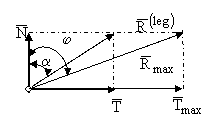a - unghiul de inclinare al reactiunii fata de directia normalei (O_n); j - unghiul de frecare de alunecare

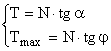          (1.111)

daca: tg j m

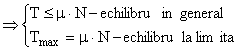            (1.112)

Echilibrul se studiaza cu relatiile:

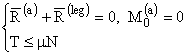                         (1.113)

3.2. Frecarea de rostogolire

Acest tip de frecare apare atunci cand torsorul de reducere al fortelor exterioare aplicate unui corp C₁ in contact cu un plan (sau un alt corp C₂) este:

            (1.114)

Torsorul fortelor de legatura va fi:

                       (1.115)

Conditiile de echilibru in acest caz vor fi:

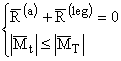(1.116)

unde:

(1.117)

s- coeficientul de frecare de rostogolire, reprezinta distanta maxima (e) cu care este deplasata reactiunea normala fata de punctul teoretic de contact O.

Pentru echilibru:

M_t ≤ N s                      (1.118)

Deosebim patru situatii:

1. M_t < s N; T < m N (corpul este si ramane in repaus);

2. M_t = s N; T < m N (corpul se rostogoleste fara alunecare);

M_t < s N; T = m N (corpul aluneca fara sa se rostogoleasca);

M_t = s N; T = m N (corpul aluneca si se rostogoleste in acelasi timp).