STUDIUL SISTEMELOR DE FORTE APLICATE SOLIDULUI RIGID

1. Generalitati

Fortele aplicate solidului rigid se reprezenta prin vectori alunecatori.

Solidul rigid: continuum material nedeformabil (distanta dintre oricare dou a puncte ale acestuia nu se modifica indiferent de miscare pe care o are sau fortele aplicate).

In Mecanica Teoretica corpurile se considera ca fiind nedeformabile.

Principiul rigiditatii:

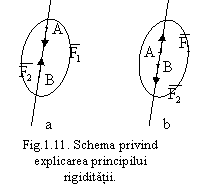
Daca asupra unui corp actioneaza doua forte si avand acelasi suport, marimile egale, dar sunt de sensuri opuse, acestea isi fac echilibru si nu modifica starea initiala de repaus sau de miscare a corpurilor.

2. Teoria Momentelor

2.1. Momentul unei forte in raport cu un punct

Fie un vector forta , aplicat intr-un punct A si un punct O in spatiu (fig.1.12).

Momentul vectorului in raport cu punctul O reprezinta produsul vectorial dintre vectorul de pozitie (distanta de la punctul de aplicatie al fortei la punctul O) si vectorul :

(1.45)

Momentul unei forte in raport cu un punct are urmatoarele caracteristici:

este un vector legat in punctul O;

este perpendicular pe planul format de suportul vectorului si punctul O;

sensul este dat de regula burghiului: se roteste burghiul in sensul dat de forta , pe directia perpendiculara pe planul [P]; sensul de inaintare al burghiului este sensul vectorului  ;

marimea vectorului :

(1.46)

unde θ este unghiul dintre si vectorul .

dimensiunea vectorului in S.I.:

                       (1.47)

Daca raportam vectorul la un sistem cartezian triortogonal drept Oxyz, notand cu (x, y, z) coordonatele punctului A si cu (X, Y, Z) componentele fortei (proiectiile ei pe axe), obtinem expresia analitica a momentului:

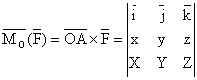(1.48)

daca:

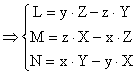(1.49)

Momentul unei forte in raport cu o axa

Fie un vector aplicat intr-un punct A si o axa (D). (fig. 1.13).

Momentul fortei in raport cu axa (D) este proiectia pe aceasta axa a momentului vectorului in raport cu oricare punct O apartinand acestei axe.

    

(1.50)

Daca am considera sistemul cartezian Oxzy, punctul A de coordonate (x, y, z) si vector de pozitie , forta avand componentele (X, Y, Z) si versorul , expresia analitica a lui va fi:

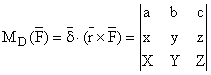(1.51)

Pentru: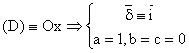     

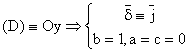
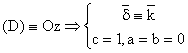
2.3. Teoremele lui Varignon

Fie n forte concurente intr-un punct O si fie un punct A oarecare in spatiu (fig.1.14).

Putem scrie:

(1.52)

Adunand relatiile (8) membru cu membru, obtinem:

                 (1.53)

Deoarece: - rezultanta sistemului de forte dat,

obtinem Teoremele lui Varignon:

1.

sau :                    (1.54)

2.                        (1.55)

Suma momentelor a n forte concurente in raport cu un punct este egala cu momentul rezultantei fortelor calculat in raport cu acel punct.

Suma momentelor a n forte concurente in raport cu o axa este egala cu momentul rezultantei fortelor luat in raport cu acea axa.

2.4. Torsorul unui sistem de forte

Fie un sistem de forte avand punctele de aplicatie . (fig. 1.15).

Putem defini:

Rezultanta sistemului de forte in punctul O, este data de relatia:

(1.56)

Momentul rezultant al sistemului de forte in punctul O:

(1.57)

Se constata ca vectorul este un vector liber, numit si primul invariant al sistemului de vectori (nu depinde de punctul O, deci ).

Vectorul depinde de punctul de reducere O deci este un vector legat de punctul O numit pol.

Se numeste torsorul sistemului de vectori forta , calculat in punctul O, sistemul format din rezultanta generala si momentul calculat in punctul O:

(1.58)

2.5. Variatia momentului rezultant la schimbarea polului de

reducere

Fie un sistem de forte aplicate in punctele A_i si punctul O (fig. 1.16).

Pentru punctul O, torsorul de reducere va fi:

(1.59)

Considerand un al doilea punct O^', torsorul de reducere al sistemului de forte in raport cu acesta va fi:

(1.60)

Deoarece si sunt vectori liberi, . Formula de schimbare a momentului la schimbarea polului de reducere, va fi:

(1.61)

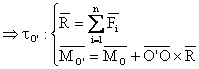(1.62)

Daca raportam sistemul la un sistem cartezian Oxyz, coordonatele punctului O' vor fi : O'(x, y, z).

Analitic:

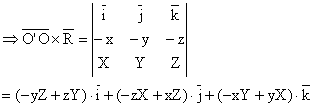
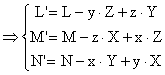(1.63)

In relatia (1.63), L', M', N'- reprezinta proiectiile pe axele sistemului ale vectorului iar L, M, N reprezinta proiectiile pe axele sistemului ale vectorului .

2.6. Torsorul minimal. Axa centrala a sistemului de forte

Reducerea unui sistem de vectori reprezinta inlocuirea acestuia cu un sistem echivalent mai simplu (calculat intr-un punct) format dintr-o rezultanta si un moment rezultant . (fig.1.17).

Putem descompune momentul in doua componente (fig.1.17):

1. - pe directia rezultantei ;

2. - pe directia normalei la directia rezultantei .

                           (1.64)

din considerente geometrice, definim momentul minim ca fiind:

(1.65)

Deci, torsorul minimal va fi:

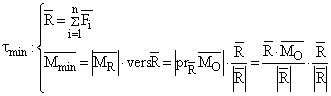(1.66)

Axa centrala locul geometric in care facand reducerea unui sistem de forte se obtine torsorul minimal.

In cazul torsorului minimal, rezultanta si momentul minim sunt doi vectori coliniari.

Fie P(x, y, z) un punct de pe axa centrala. Momentul in acest punct al sistemului de forte se poate scrie:

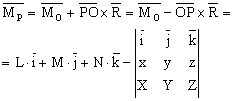
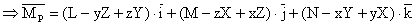    (1.67)

Tinand cont ca:

(1.68)

Relatia (1.68) reprezinta ecuatiile axei centrale a sistemului de vectori.

2.7. Reducerea unui sistem de vectori alunecatori

Exista trei cazuri de reducere:

Cazul I: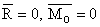

Torsorul de reducere este nul.

Sistemul este in echilibru. Un astfel de sistem se numeste echivalent cu zero.

Cazul II: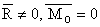

Sistemul este echivalent cu un vector unic aplicat in O.

Torsorul de reducere este doar rezultanta .

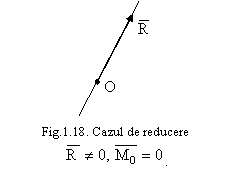
Cazul III:

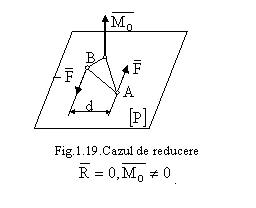Sistemul este echivalent cu un cuplu (doi vectori egali ca marime, paraleli si de sensuri contrare). Momentul cuplului va fi: (fig.1.19).

Cazul IV:

. (fig. 1.20)

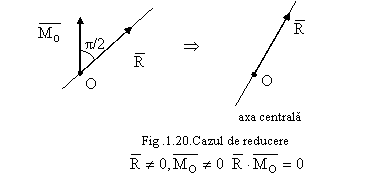
Torsorul este:

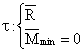
si fac intre ele un unghi α ≠ π/2

Torsorul este
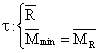